Primers • Activation Functions
- Overview
- Sigmoid Function
- Hyperbolic Tangent (tanh):
- Rectified Linear Unit (ReLU):
- Softmax:
- Further Reading
Overview
- Activation functions play a crucial role in neural networks by determining whether a neuron should be ‘activated’ or not. They introduce non-linearity, allowing neural networks to model complex, non-linear relationships. They are applied to the output of each neuron in a neural network and decide whether the neuron is critical to the network or not.
- Let’s explore some commonly used activation functions and their characteristics.
Sigmoid Function
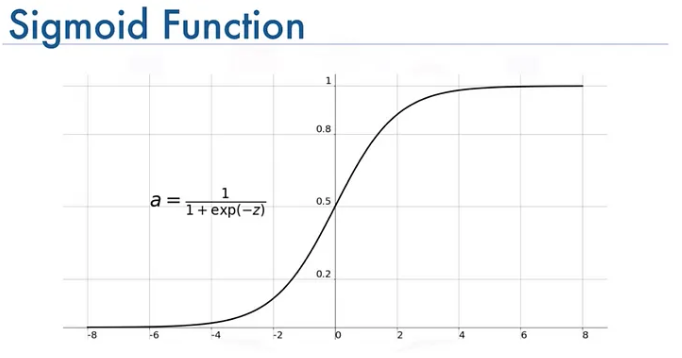
- The sigmoid function is often used for binary classification problems. It maps any real-valued number to the range (0, 1), providing an output that can be interpreted as a probability.
- However, the sigmoid function has some drawbacks, such as gradient saturation and slow convergence.
- Sigmoid is defined as \(sigmoid(x) = 1 / (1 + exp(-x))\)

Hyperbolic Tangent (tanh):
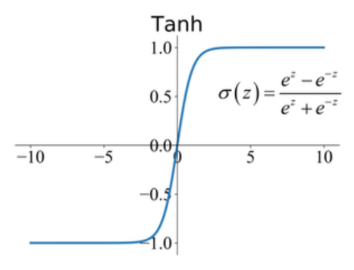
- The hyperbolic tangent function maps inputs to values between -1 and 1. It is often used to model continuous outputs in the range [-1, 1]. Tanh is suitable for tasks such as modeling sequential data in recurrent neural networks (RNNs) and long short-term memory (LSTM) networks.
- For example, it is commonly used in recurrent neural networks (RNNs) and long short-term memory (LSTM) networks to model sequential data.
- “Historically, the tanh function became preferred over the sigmoid function as it gave better performance for multi-layer neural networks.
- But it did not solve the vanishing gradient problem that sigmoids suffered, which was tackled more effectively with the introduction of ReLU activations.” Source
- Hyperbolic Tangent is defined as: \(tanh(x) = (exp(x) - exp(-x)) / (exp(x) + exp(-x))\)
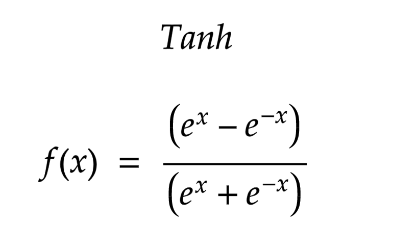
Rectified Linear Unit (ReLU):
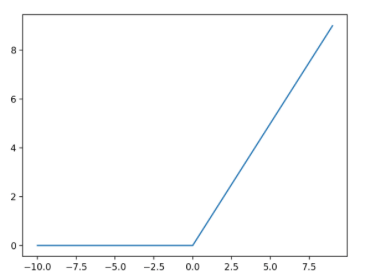
- ReLU is a popular activation function used in the hidden layers of feedforward neural networks. It outputs 0 for negative input values and leaves positive values unchanged.
- ReLU activations address the vanishing gradient problem that sigmoid activations suffer from.
- ReLU is defined as:
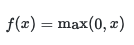
Leaky ReLU:
- Leaky ReLU is a variant of ReLU that introduces a small, non-zero slope for negative inputs. This prevents complete saturation of negative values and is useful in scenarios where sparse gradients may occur, such as training generative adversarial networks (GANs).
- It is defined as max(αx, x), where x is the input and α is a small positive constant.
- “Leaky Rectified Linear Unit, or Leaky ReLU, is a type of activation function based on a ReLU, but it has a small slope for negative values instead of a flat slope. The slope coefficient is determined before training, i.e. it is not learnt during training.
- This type of activation function is popular in tasks where we may suffer from sparse gradients, for example training generative adversarial networks.”Source
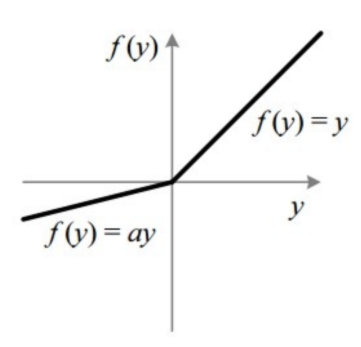
Softmax:
- Now here is where the confusion intensifies because we have a Softmax-Loss as well as a Softmax activation function and we will explain it in more detail further below.
- The softmax function is an activation function often used in the output layer of a neural network for multi-class classification problems. It transforms the raw score outputs from the previous layer into probabilities that sum up to 1, giving a distribution of class probabilities.
- Cross-entropy loss is a popular loss function for classification tasks, including multi-class classification. It measures the dissimilarity between the predicted probability distribution (often obtained by applying the softmax function to the raw output scores) and the actual label distribution.
- Sometimes, the combination of softmax activation and cross-entropy loss is collectively referred to as “Softmax Loss” or “Softmax Cross-Entropy Loss”.
- This naming can indeed cause some confusion, as it’s not the softmax function itself acting as the loss function, but rather the cross-entropy loss applied to the outputs of the softmax function.
- The softmax function is indeed differentiable, which is vital for backpropagation and gradient-based optimization algorithms in training neural networks.
-
Softmax is defined as: \(softmax(x_i) = exp(x_i) / sum(exp(x_j)) for all x_j in the input vector\)
