Primers • Mixture of Experts
- Overview
- Overview
- Mixture-of-Experts: The Classic Approach
- The Deep Learning Way
- Expert Choice Routing
- Implications and Outlooks
- The “How” Behind MoE
- What’s Next?
- Citation
Overview
- Artificial neural networks have emerged as the cornerstone of deep learning, offering a remarkable way of drawing valuable insights from a plethora of data. However, the efficacy of these neural networks hinges heavily on their parameter count. Mixture-of-Experts (MoE) presents an efficient approach to dramatically increasing a model’s capabilities without introducing a proportional amount of computational overhead.
- Originally proposed in 1991 by Robert A. Jacobs et al., MoE adopts a conditional computation paradigm by only selecting parts of an ensemble, referred to as experts, and activating them depending on the data at hand. The MoE structure appeared long before the popularization of deep learning.
Overview
- Artificial neural networks have emerged as the cornerstone of deep learning, offering a remarkable way of drawing valuable insights from a plethora of data. However, the efficacy of these neural networks hinges heavily on their parameter count. Mixture-of-Experts (MoE) presents an efficient approach to dramatically increasing a model’s capabilities without introducing a proportional amount of computational overhead.
- Originally proposed in 1991 by Robert A. Jacobs et al., MoE adopts a conditional computation paradigm by only selecting parts of an ensemble, referred to as experts, and activating them depending on the data at hand. The MoE structure appeared long before the popularization of deep learning.
Mixture-of-Experts: The Classic Approach
- The MoE concept is a type of ensemble learning technique initially developed within the field of artificial neural networks. It introduces the idea of training experts on specific subtasks of a complex predictive modeling problem.
- In a typical ensemble scenario, all models are trained on the same dataset, and their outputs are combined through simple averaging, weighted mean, or majority voting. However, in Mixture-of-Experts (MoE), each “expert” model within the ensemble is only trained on a subset of data where it can achieve optimal performance, thus narrowing the model’s focus. Put simply, MoE is an architecture that divides input data into multiple sub-tasks and trains a group of experts to specialize in each sub-task. These experts can be thought of as smaller, specialized models that are better at solving their respective sub-tasks.
- The popularity of MoE only rose recently as the appearance of Large Language Models (LLMs) and transformer-based models in general swept through the machine learning field. Consequently, this is because of modern datasets’ increased complexity and size. Each dataset contains different regimes with vastly different relationships between the features and the labels.
- To appreciate the essence of MoE, it is crucial to understand its architectural elements:
- Division of dataset into local subsets: First, the predictive modeling problem is divided into subtasks. This division often requires domain knowledge or employs an unsupervised clustering algorithm. It’s important to clarify that clustering is not based on the feature vectors’ similarities. Instead, it’s executed based on the correlation among the relationships that the features share with the labels.
- Expert Models: These are the specialized neural network layers or experts that are trained to excel at specific sub-tasks. Each expert receives the same input pattern and processes it according to its specialization. Put simply, an expert is trained for each subset of the data. Typically, the experts themselves can be any model, from Support Vector Machines (SVM) to neural networks. Each expert model receives the same input pattern and makes a prediction.
- Gating Model (Router): The gating model/network, also called the MoE layer or Router, is responsible for selecting which experts to use for each input data. It works by estimating the compatibility between the input data and each expert, and then outputs a softmax distribution over the experts. This distribution is used as the weights to combine the outputs of the expert layers. Put simply, this model helps interpret predictions made by each expert and decide which expert to trust for a given input.
- Pooling Method: Finally, an aggregation mechanism is needed to make a prediction based on the output from the gating network and the experts.
- The gating network and expert layers are jointly trained to minimize the overall loss function of the MoE model. The gating network learns to route each input to the most relevant expert layer(s), while the expert layers specialize in their assigned sub-tasks.
- This divide-and-conquer approach effectively delegates complex tasks to experts, enabling efficient processing and improved accuracy.
Put simply, a Mixture of Experts (MoE) is how an ensemble of AI models decides as one.
The Deep Learning Way
- In 2017, an extension of the MoE paradigm suited for deep learning was proposed by Noam Shazeer et al.
- In most deep learning models, increasing model capacity generally translates to improved performance when datasets are sufficiently large. Generally, when the entire model is activated by every example, it can lead to “a roughly quadratic blow-up in training costs, as both the model size and the number of training examples increase”, stated by Shazeer et al.
- Although the disadvantages of dense models are clear, there have been various challenges for an effective conditional computation method targeted toward modern deep learning models, mainly for the following reasons:
- Modern computing devices like GPUs and TPUs perform better in arithmetic operations than in network branching.
- Larger batch sizes benefit performance but are reduced by conditional computation.
- Network bandwidth can limit computational efficiency, notably affecting embedding layers.
- Some schemes might need loss terms to attain required sparsity levels, impacting model quality and load balance.
- Model capacity is vital for handling vast data sets, a challenge that current conditional computation literature doesn’t adequately address.
- The MoE technique presented by Shazeer et al. aims to achieve conditional computation while addressing the abovementioned issues. They could increase model capacity by more than a thousandfold while only sustaining minor computational efficiency losses.
- The authors introduced a new type of network layer called the “Sparsely-Gated Mixture-of-Experts Layer.” They are built on previous iterations of MoE and aim to provide a general-purpose neural network component that can be adapted to different types of tasks.
- The Sparsely-Gated Mixture-of-Experts Layer, or the MoE layer, consists of numerous expert networks, each being a simple feed-forward neural network and a trainable gating network. The gating network is responsible for selecting a sparse combination of these experts to process each input.
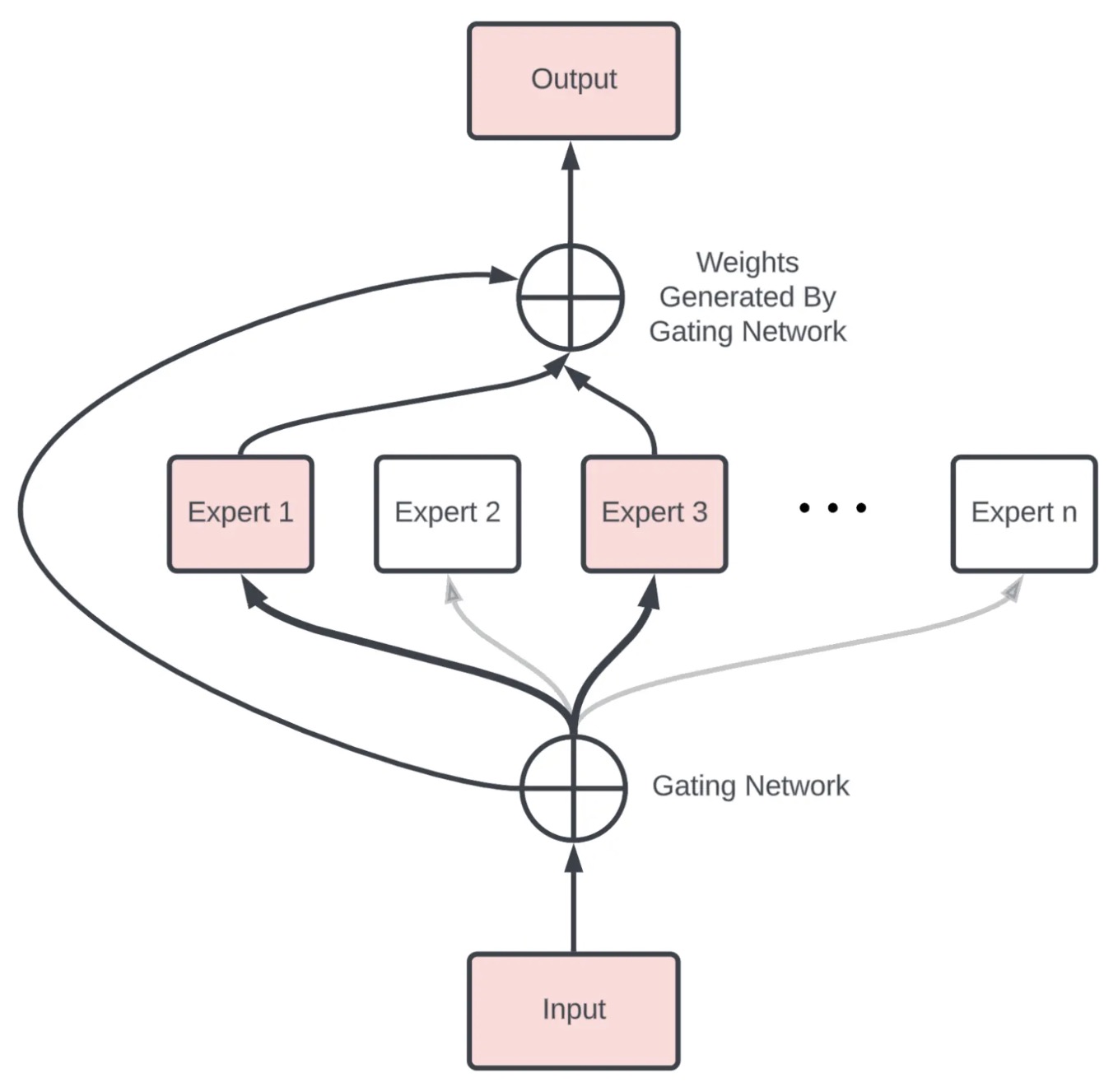
- The fascinating feature here is the use of sparsity in the gating function. This means that for every input instance, the gating network only selects a few experts for processing, keeping the rest inactive. This sparsity and expert selection is achieved dynamically for each input, making the entire process highly flexible and adaptive. Notably, the computational efficiency is preserved since inactive parts of the network are not processed.
- The MoE layer can be stacked hierarchically, where the primary MoE selects a sparsely weighted combination of “experts.” Each combination utilizes a MoE layer.
- Moreover, the authors also introduced an innovative technique called Noisy Top-\(K\) Gating. This mechanism adds a tunable Gaussian noise to the gating function, retains only the top K values, and assigns the rest to negative infinity, translating to a zero gating value. Such an approach ensures the sparsity of the gating network while maintaining robustness against potential discontinuities in the gating function output. Interestingly, it also aids in load balancing across the expert networks.
- In their framework, both the gating network and the experts are trained jointly via back-propagation, the standard training mechanism for neural networks. The output from the gating network is a sparse, n-dimensional vector, which serves as the gate values for the n-expert networks. The output from each expert is then weighted by the corresponding gating value to produce the final model output.
Expert Choice Routing
- Despite the popularity of MoE in recent transformer-based models demonstrated by the Switch Transformer, GLaM, V-MoE, and FLAN-MoE, improvements and research potentials remain in the area.
- In any case of a MoE scheme, the routing or gating function may cause specific experts to be undertrained as it overfits other experts. Regularization has been introduced to avoid too many examples being routed to a single or a particular subset of experts. Additionally, Google Research proposed “Expert Choice Routing” in November 2022, aiming to improve upon the potential flaw and explicitly targeting language models.
- Unlike traditional MoE models, the EC routing method is founded on a different approach to assigning “experts” to “tokens” within a Mixture-of-Experts (MoE) model. Instead of assigning tokens to experts as traditional MoE models do, EC reverses this process, assigning experts to tokens based on their importance or difficulty.
- EC routing sets an “expert capacity” value to regulate how many tokens an expert can handle simultaneously. It’s calculated as the average number of tokens per expert in a batch of input sequences, which is then multiplied by a “capacity factor”. The capacity factor is a variable that determines the average number of experts each token can be assigned to. By adjusting the capacity factor, researchers can control how many experts work on each token, providing flexibility in allocating computation resources.
- To decide which tokens should be assigned to which experts, the EC method uses a “token-to-expert score matrix.” This matrix scores the compatibility between each token and each expert, ranking which experts would best fit each token. Based on these scores, the most relevant tokens for each expert are selected via a “top-k function”. The k here refers to the number of tokens chosen for each expert.
- Once the most relevant tokens have been identified for each expert, a permutation function is applied to arrange the data. This means reshuffling the data so that each expert gets its assigned tokens, allowing for efficient parallel computation across all the experts.
Implications and Outlooks
- Incorporating MoE into deep learning is a relatively new development, gaining traction only as models for NLP and computer vision tasks began to scale significantly. Before this, the demand for conditional computation was less pronounced than it is for contemporary Large Language Models (LLM) and intricate CNNs.
- In 2021, Meta AI conducted a dedicated study for MoE models trained on language data, comparing how MoE models scale in comparison with dense models. They found that other than fine-tuning, MoE-based models can match the performance of dense models with a quarter of the computing. They could scale MoE models up to a trillion parameters (this was long before GPT-4 was released) and consistently outperform their dense model counterparts.
- The same year, Google Brain proposed V-MoE, a vision transformer utilizing sparse MoE layers. They found that V-MoE can match the performance of state-of-the-art models with as little as half of the computational resources required.
- More famously, GPT-4 was also leaked to be adopting a MoE scheme with 8 local models, each containing 220 billion parameters, totaling a whopping 1.7 trillion parameters.
The “How” Behind MoE
- Although the success of MoE is clear in the deep learning field, as with most things in deep learning, our understanding of how it can perform so well is rather unclear.
- Notably, each expert model is initialized and trained in the same manner, and the gating network is typically configured to dispatch data equally to each expert. Unlike traditional MoE methods, all experts are trained jointly with the MoE layer on the same dataset. It is fascinating how each expert can become “specialized” in their own task, and experts in MoE do not collapse into a single model.
- The paper “Towards Understanding Mixture of Experts in Deep Learning” by Zixiang Chen et al. attempts to interpret the “hows” behind MoE layers. They conclude that the “cluster structure of the underlying problem and the non-linearity of the expert is pivotal to the success of MoE.”
- Although the conclusion does not provide a direct answer, it helps to gain more insight into the simple yet effective approach of MoE.
What’s Next?
- Theoretically, a deeper understanding of MoE architectures and their working principles is needed. As we saw in Chen et al.’s paper, the reasons behind the success of MoE layers are still partially obscure. Therefore, more theoretical and empirical research is required to demystify the intrinsic mechanics of these models, potentially leading to their optimization and better generalization.
- Additionally, how to design more effective gating mechanisms and expert models is an open question with great potential for future exploration. While Expert Choice Routing offers a promising direction, other innovative approaches might enhance the routing mechanism.
- Lastly, while MoE has shown impressive results in domains like NLP and computer vision, there is considerable room to explore its utility in other domains, such as reinforcement learning, tabular data domains, and more.
- The journey of MoE is in its infancy in the realm of deep learning, with many milestones yet to be achieved. However, its potential for transforming how we understand and deploy deep learning models is enormous. With the current state of computing, it’s unlikely that we will see significant improvements to hardware as rapidly as we see improvements to modeling techniques. By leveraging the inherent strength of the MoE paradigm—the division of complex tasks into simpler subtasks handled by specialized expert models—we may continue to push the boundaries of what is achievable with deep learning. And that, indeed, is an exciting prospect to look forward to.
Citation
If you found our work useful, please cite it as:
@article{Chadha2020DistilledLossFunctions,
title = {Loss Functions},
author = {Chadha, Aman and Jain, Vinija},
journal = {Distilled AI},
year = {2020},
note = {\url{https://vinija.ai}}
}