Token Sampling Methods
- Overview
- Background
- Related: Temperature
- Greedy Decoding
- Exhaustive Search Decoding
- Beam Search
- Constrained Beam Search
- Top-\(k\)
- Top-\(p\) (nucleus sampling)
- Greedy vs. top-\(k\) and top-\(p\)
- Nucleus sampling v/s Temperature
- References
Overview
- The method of selecting output tokens (specifically called token sampling methods or decoding strategies) is a key concept in text generation with language models.
- To grasp the technical underpinnings of token sampling, it’s helpful to know why Large Language Models (LLMs) work as well as they do. These systems understand input and output text as strings of “tokens,” which can be words but also punctuation marks and parts of words.
- At their core, the systems are constantly generating a mathematical function called a probability distribution to decide the next token (e.g. word) to output, taking into account all previously outputted tokens.
- In the case of OpenAI-hosted systems like ChatGPT, after the distribution is generated, OpenAI’s server does the job of sampling tokens according to the distribution. There’s some randomness in this selection; that’s why the same text prompt can yield a different response.
- In this article, we will talk about different token sampling methods and related concepts such as Temperature, Greedy Decoding, Exhaustive Search Decoding, Beam Search, top-\(k\), and top-\(p\).
Background
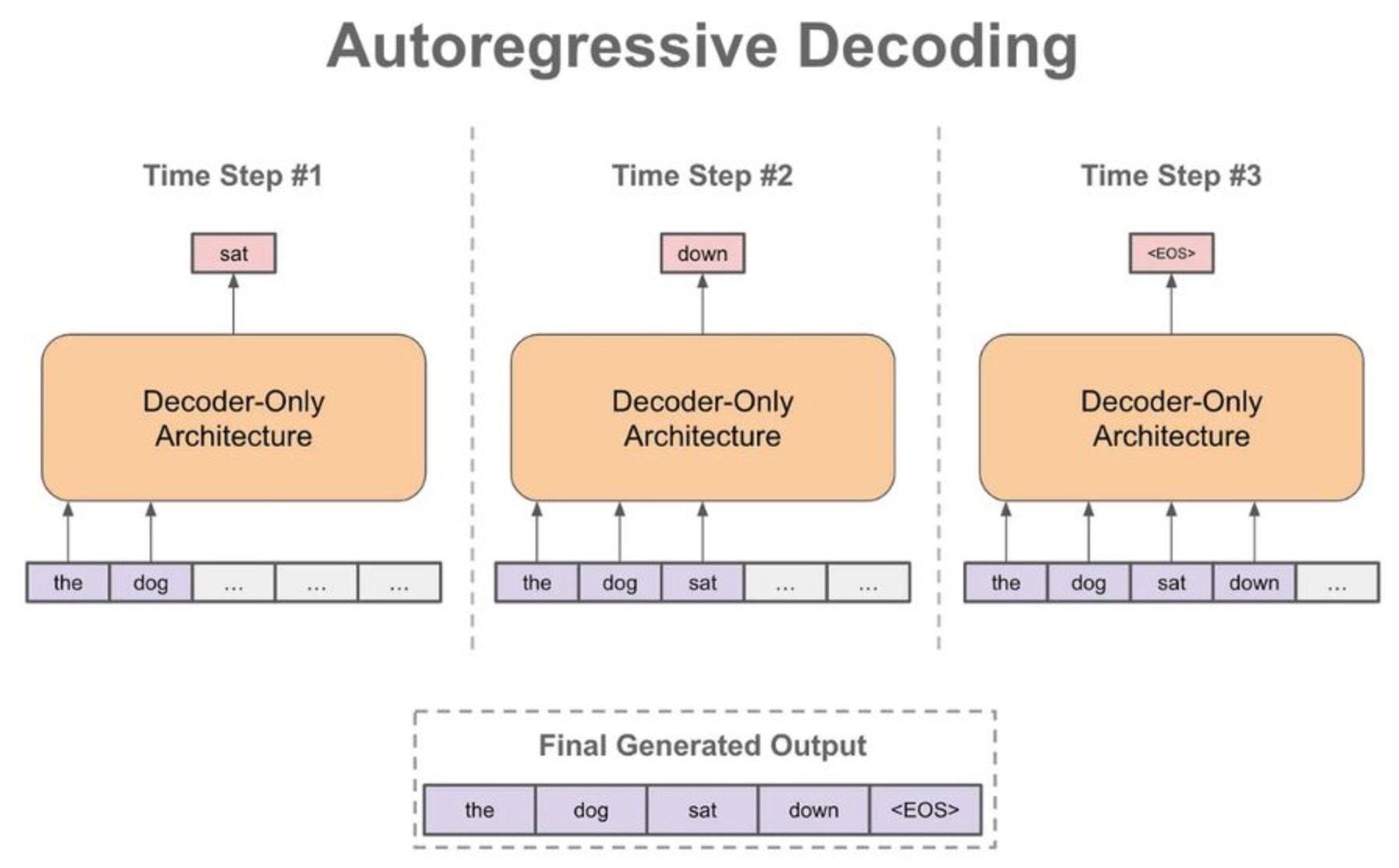
Autoregressive decoding
-
When we generate a textual sequence with a language model, we typically begin with a textual prefix/prompt. Then, we follow the steps shown below:
- Use the language model to generate the next token.
- Add this output token to our input sequence.
- Repeat.
-
By continually generating the next token in this manner (i.e., this is what we call the autoregressive decoding process), we can generate an entire textual sequence (cf. below image; source).
Token probabilities
- But, how do we choose/predict the next token (i.e., step one shown above)?
- Instead of directly outputting the next token, language models output a probability distribution over the set of all possible tokens. Put simply, LLMs are essentially neural networks tackling a classification problem over the vocabulary (unique tokens).
- Given this probability distribution, we can follow several different strategies for selecting the next token. For example, greedy decoding (one potential strategy), as we’ll see below, simply selects the token with the highest probability as the next token.
Logits and Softmax
-
LLMs produce class probabilities with logit vector \(\mathbf{z}\) where \(\mathbf{z}=\left(z_{1}, \ldots, z_{n}\right)\) by performing the softmax function to produce probability vector \(\mathbf{q}=\left(q_{1}, \ldots, q_{n}\right)\) by comparing \(z_{i}\) with with the other logits.
\[q_{i}=\frac{\exp \left(z_{i}\right)}{\sum_{j} \exp \left(z_{j}\right)}\] -
The softmax function normalizes the candidates at each iteration of the network based on their exponential values by ensuring the network outputs are all between zero and one at every timestep, thereby easing their interpretation as probability values (cf. below image; source).

Related: Temperature
- While temperature is not a token sampling method per se, it impacts the process of token sampling and is thus included in this article.
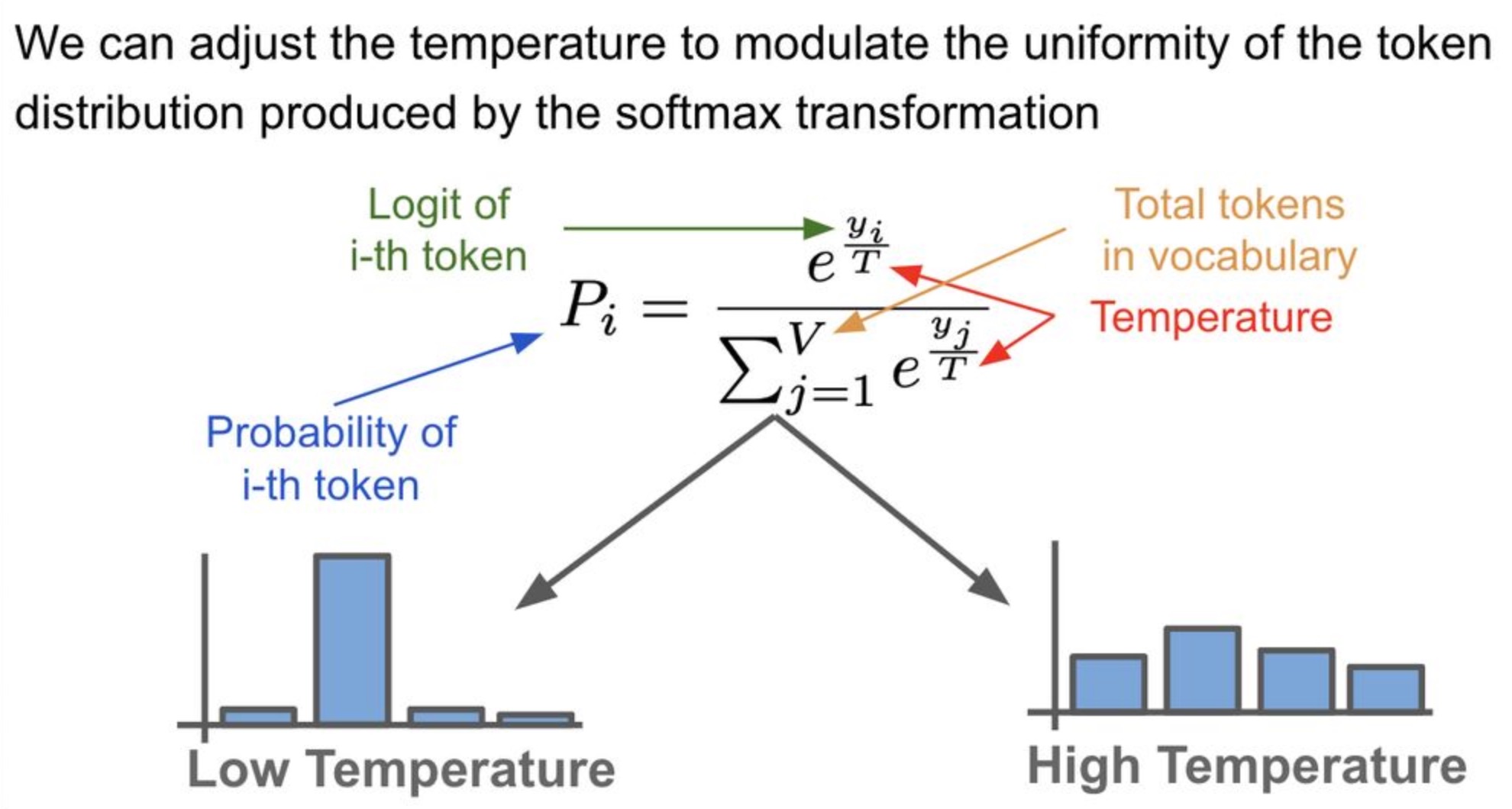
- We can leverage the temperature setting to “tweak” the probability distribution over tokens. Temperature is simply a hyperparameter
-
Temperature is a hyperparameter in the softmax transformation (cf. below image; source) used to generate the token probability distribution which influences the randomness of predictions by scaling the logits before applying softmax.
- For example, in TensorFlow’s Magenta implementation of LSTMs, temperature represents how much to scale/divide the logits by before computing the softmax.
-
The “vanilla” softmax function in the Logits and Softmax section incorporates the temperature hyperparameter \(T\) as follows:
\[q_{i}=\frac{\frac{\exp z_{i}}{T}}{\sum_{j} \frac{\exp z_{j}}{T}}\]- where \(T\) is the temperature parameter (set to 1 by default).
- When the temperature is 1, we compute the softmax directly on the logits (the unscaled output of earlier layers), and using a temperature of 0.6 the model computes the softmax on \(\frac{\text { logits }}{0.6}\), resulting in a larger value. Performing softmax on larger values makes the model more confident (less input is needed to activate the output layer) but also more conservative in its samples (it is less likely to sample from unlikely candidates).
- Using a higher temperature produces a softer probability distribution over the classes, and makes the RNN more “easily excited” by samples, resulting in more diversity/randomness in its tokens (thus enabling it to get out of repetitive loops easily) but also leads to more mistakes.
- A higher temperature therefore increases the sensitivity to low probability candidates. The output candidate or sample can be a letter, word, pixel, musical note, etc. depending on the classification task at hand.
- From the Wikipedia article on softmax function:
For high temperatures \((\tau \rightarrow \infty\)), all samples have nearly the same probability and the lower the temperature, the more expected rewards affect the probability. For a low temperature \(\left(\tau \rightarrow 0^{+}\right)\) , the probability of the sample with the highest expected reward tends to 1.
Greedy Decoding
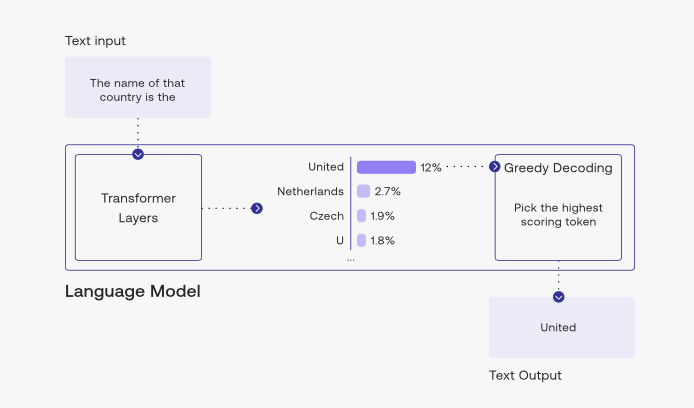
- Greedy decoding uses
argmaxto select the output with the highest probability at each step during the decoding process. - The problem with this method is, it has no way to revert back in time and rectify previously generated tokens to fix its output. For example, if the machine translation prompt is “il a m’entarté” (he hit me with a pie) and greedy decoding translation generates “he hit a”, it has no way of going back to replace “a” with “me”. Greedy decoding chooses the most probable output at each time step, without considering the future impact of that choice on subsequent decisions.
- During the decoding process, the model generates a sequence of words or tokens one at a time, based on the previously generated words and the input sequence. In greedy decoding, usually we decode until the model produces a
<END>token, For example:<START>he hit me with a pie<END>source - While greedy decoding is computationally efficient and easy to implement, it may not always produce the best possible output sequence.
- A way to mitigate the issues we see from greedy decoding is to use exhaustive search decoding or beam search.
- The image below (source) shows greedy decoding in action, picking the top token at each interval.
Exhaustive Search Decoding
- Exhaustive search, as the name suggests, considers every possible combination or permutation of output sequences and selecting the one that yields the highest score according to a given objective function.
- In the context of sequence-to-sequence models such as neural machine translation, exhaustive search decoding involves generating every possible output sequence and then evaluating each one using a scoring function that measures how well the output sequence matches the desired output. This can be a computationally intensive process, as the number of possible output sequences grows exponentially with the length of the input sequence.
- Exhaustive search decoding can produce highly accurate translations or summaries, but it is generally not feasible for most real-world applications due to its computational complexity.
- This would result in a time complexity of \(O(V^{(T)})\) where \(V\) is the vocab size and \(T\) is the length of the translation and as we can expect, this would be too expensive.
Beam Search
- Beam search is a search algorithm, frequently used in machine translation tasks, to generate the most likely sequence of words given a particular input or context. It is an efficient algorithm that explores multiple possibilities and retains the most likely ones, based on a pre-defined parameter called the beam size.
- Beam search is widely used in sequence-to-sequence models, including recurrent neural networks and transformers, to improve the quality of the output by exploring different possibilities while being computationally efficient.
- The core idea of beam search is that on each step of the decoder, we want to keep track of the \(k\) most probable partial candidates/hypotheses (such as generated translations in case of a machine translation task) where \(k\) is the beam size (usually 5 - 10 in practice). Put simply, we book-keep the top \(k\) predictions, generate the word after next for each of these predictions, and select whichever combination had less error.
- The image below (source) shows how the algorithm works with a beam size of 2.
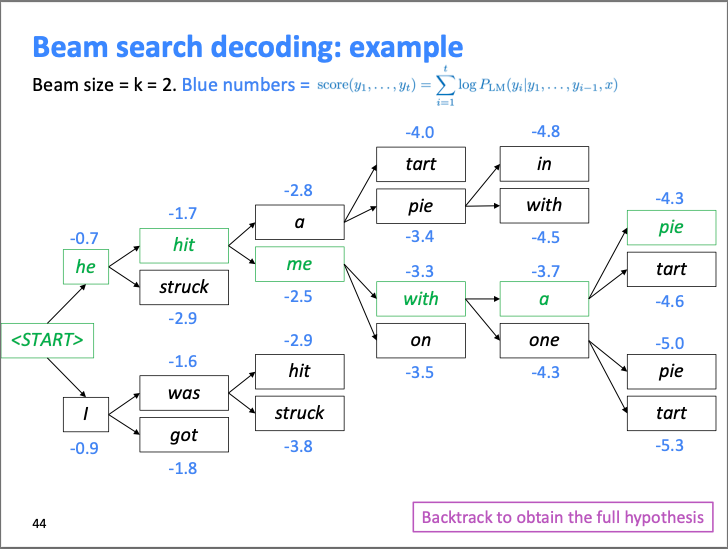
- We can see how at each step, it calculates two most probable options along with their score, and creates the top scoring hypothesis (best guess of the likely sequence). It will then backtrack to obtain the full hypothesis.
- In beam search decoding, different hypotheses may produce
<END>tokens on different timesteps - When a hypothesis produces
<END>, that hypothesis is complete so we place it aside and continue exploring other hypotheses via beam search. - Usually we continue beam search until:
- We reach timestep \(T\) (where \(T\) is some pre-defined cutoff), or
- We have at least \(n\) completed hypotheses (where n is pre-defined cutoff).
- So now that we have a list of completed hypotheses, how do we select the one with the highest score that fits our task the best?
- It’s to be noted that the longer hypotheses have lower scores, so simply selecting the largest score may not work. Thus, we need to normalize the hypotheses by length and then use this to select the top one.
- Note, hypothesis here is the \(k\) most probable partial translation (if the task is machine translation) and has a score which is the log probability. Since the log of a number \(\in [0 ,1]\) falls under \([-\infty, 0]\), all the scores are non-positive and a higher score the hypothesis has, the better it is.
- Additionally, beam search is not guaranteed to find the optimal solution, but it is more efficient than conducting an exhaustive search.
- For more details, please refer D2L.ai: Beam Search.
Constrained Beam Search
- Constrained beam search allows more control over the output that is generated, which is especially useful, for example, if your task is Neural Machine Translation and you have certain words that will need to be in the output.
- In constrained beam search, additional constraints are imposed on the generated sequences to ensure that they adhere to certain criteria or rules.
- The basic idea of constrained beam search is to modify the traditional beam search algorithm to incorporate constraints while generating sequences. This can be done by maintaining a set of active beams that satisfy the constraints during the search process. At each step, the algorithm generates and scores multiple candidate sequences, and then prunes the candidates that violate the constraints. The remaining candidates are then used to generate the next set of candidates, and the process continues until a complete sequence that satisfies the constraints is generated, or until a predefined stopping criterion is met.
- Constrained beam search requires careful management of the constraints to ensure that they are satisfied while still maintaining a diverse set of candidate sequences. One common approach is to use penalty functions or heuristics to discourage or penalize candidates that violate the constraints, while still allowing them to be considered during the search process. Another approach is to use a separate constraint satisfaction module that guides the search process by providing additional information or feedback on the constraints.
- For example, in text generation, constraints could include limitations on the length of the generated text, adherence to a particular format or structure, or inclusion of certain keywords or phrases. Constrained beam search modifies the scoring function or introduces additional checks during the search process to ensure that only valid sequences that meet the constraints are considered and expanded.
- Constrained beam search is commonly used in tasks such as text summarization, machine translation, and dialogue generation, where it is important to generate sequences that adhere to certain rules, guidelines, or restrictions while maintaining fluency and coherence in the generated output. It is a useful technique for controlling the output of a sequence generation model and ensuring that the generated sequences meet specific criteria or constraints.
- In the traditional beam search setting, we find the top \(k\) most probable next tokens at each branch and append them for consideration. In the constrained setting, we do the same but also append the tokens that will take us closer to fulfilling our constraints.
- The image below (source) shows step 1 of constrained beam search working in action. “On top of the usual high-probability next tokens like “dog” and “nice”, we force the token “is” in order to get us closer to fulfilling our constraint of “is fast”.” (source)
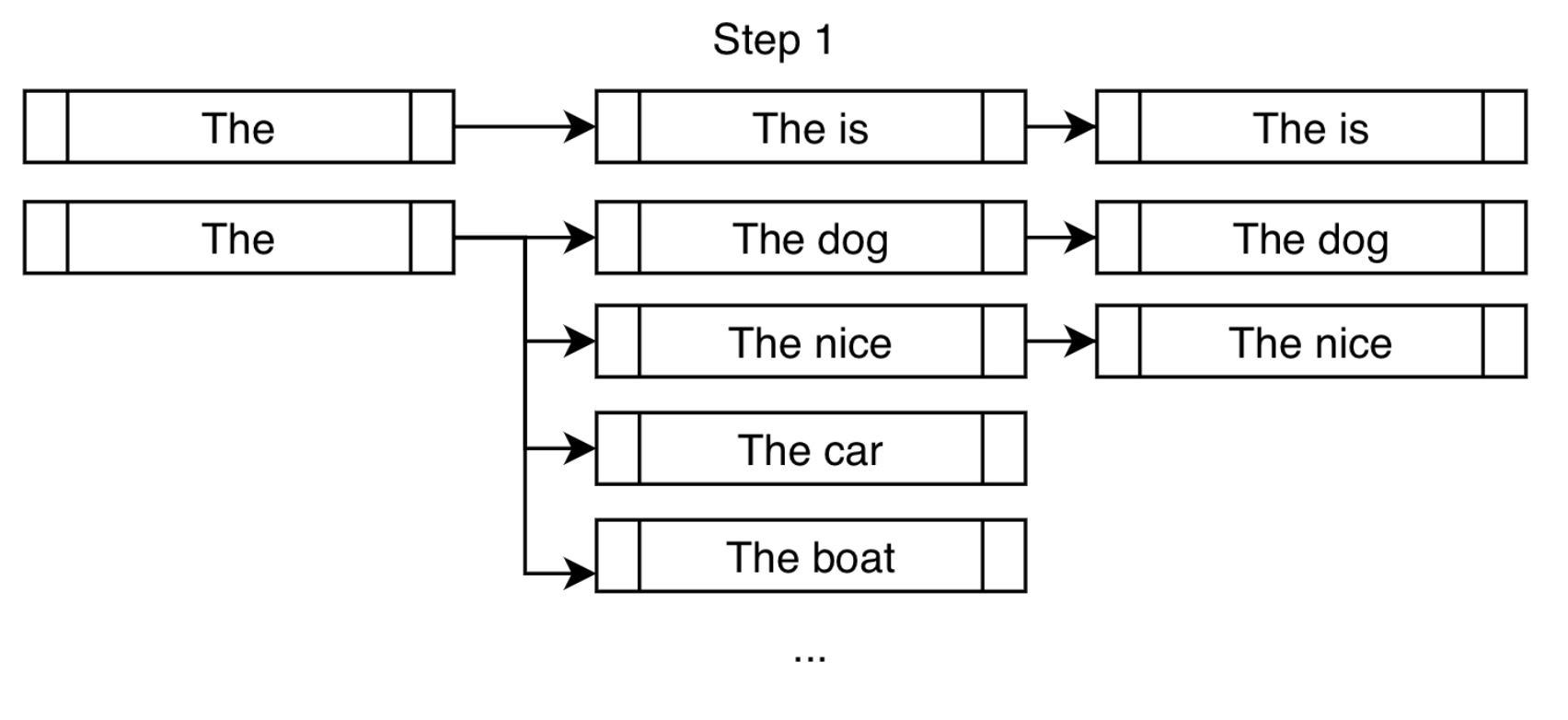
Banking
- Now a practical next question would be, wouldn’t forcing a token create nonsensical outputs? Using banks solves this problem by creating a balance between fulfilling the constraints and creating sensible output, and we can see this illustrated in the figure below (source):
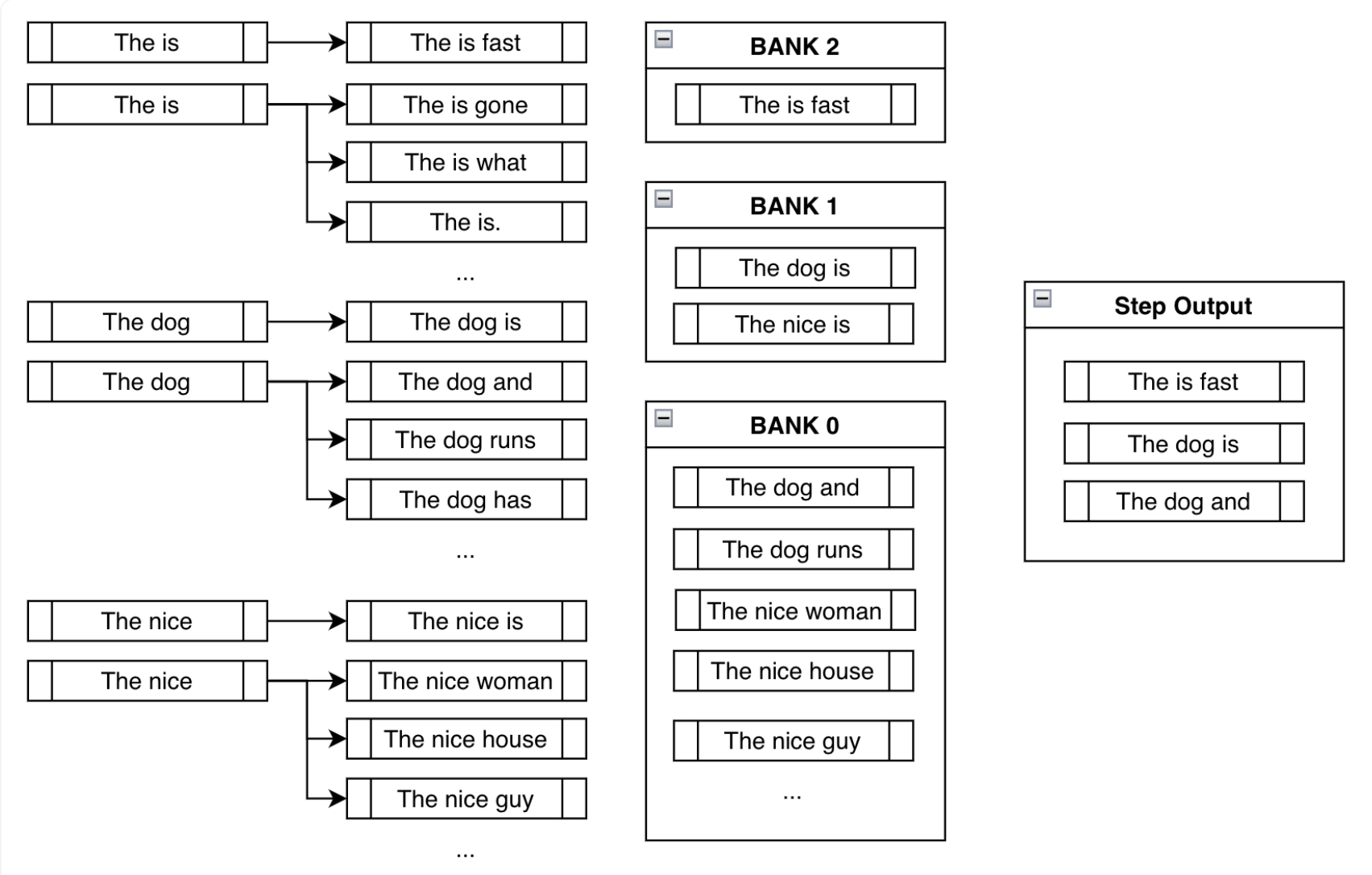
- “After sorting all the possible beams into their respective banks, we do a round-robin selection. With the above example, we’d select the most probable output from Bank 2, then most probable from Bank 1, one from Bank 0, the second most probable from Bank 2, the second most probable from Bank 1, and so forth. Assuming we’re using three beams, we just do the above process three times to end up with
["The is fast", "The dog is", "The dog and"].” (source) - Thus, even though we are forcing tokens on the model, we are still keeping track of other high probable sequences that are likely not nonsensical.
- The image below (source) shows the result and all the steps combined.
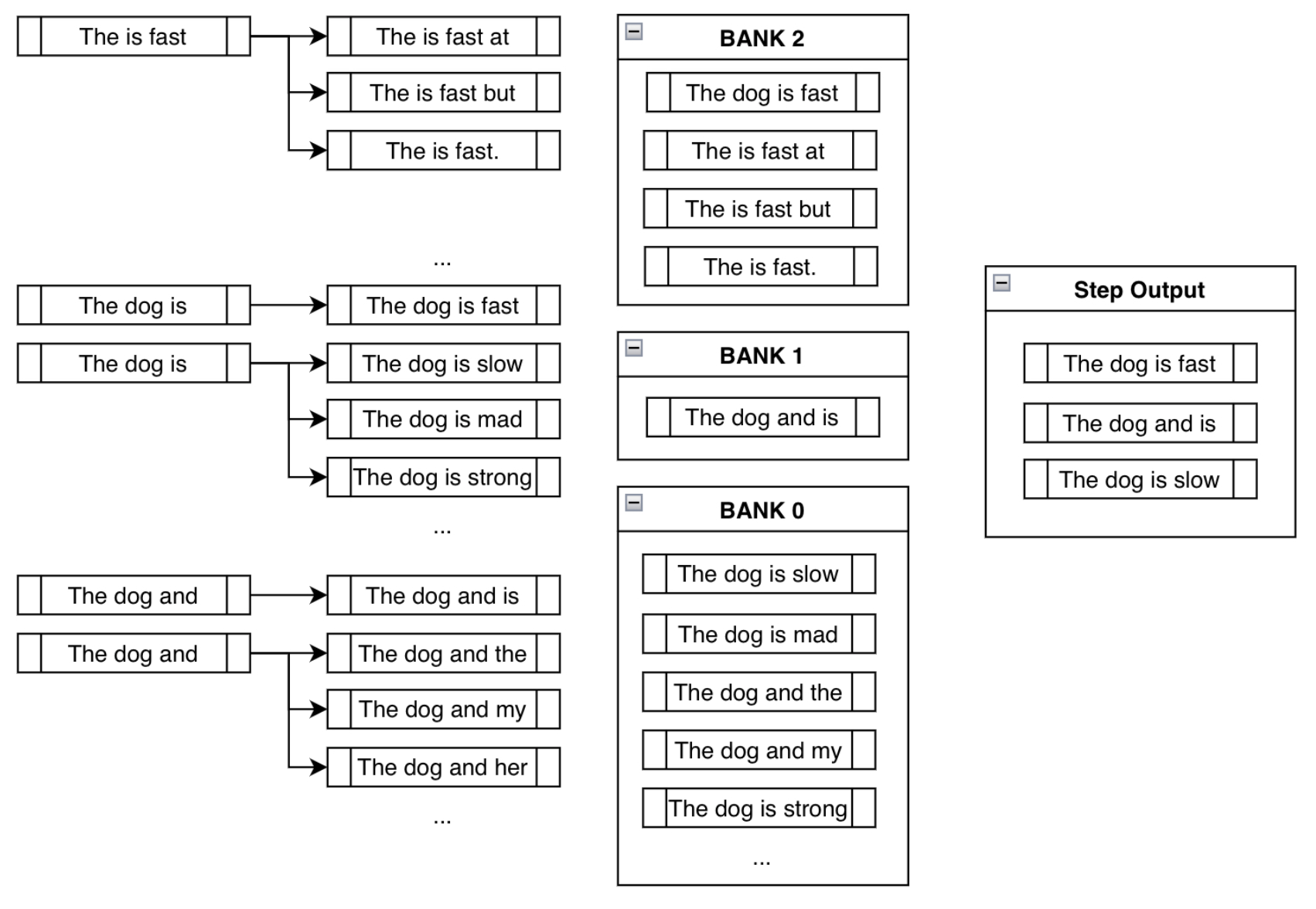
Top-\(k\)
- Top \(k\) uses a strategy where it allows to sample from a shortlist of top \(k\) tokens. This allows all top k players to be given a chance of being chosen as the next token.
- In top-\(k\) sampling, once the top \(k\) most probable tokens are selected at each time step, the choice among them could be based on uniform sampling (each of the top-\(k\) tokens has an equal chance of being picked) or proportional to their calculated probabilities.
The choice between uniform and proportional selection in top-\(k\) sampling depends on the desired balance between diversity and coherence in the generated text. Uniform sampling promotes diversity by giving equal chance to all top \(k\) tokens, while proportional sampling favors coherence and contextual relevance by weighting tokens according to their probabilities. The specific application and user preference ultimately dictate the most suitable approach.
- It is suitable for tasks that require a balance between diversity and control over the output, such as text generation and conversational AI.
- Note, if \(k\) is set to 1, it is essentially greedy decoding which we saw in one of the earlier sections.
- The image below (source) shows top-\(k\) in action for \(k = 3\).
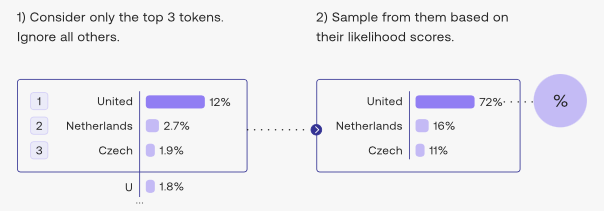
- Additionally, it’s important to note that the smaller the \(k\) you choose, the narrower the selection will become (thus, reduced diversity, more control) and conversely, the higher the \(k\) you choose, the wider the selection will become (thus, increased diversity, less control).
Top-\(p\) (nucleus sampling)
- The difficulty of selecting the best value of \(k\) in case of top-\(k\) sampling opens the door for a popular decoding strategy that dynamically sets the size of the shortlist of tokens. This method, called top-\(p\) or nucleus sampling, shortlists the top tokens whose sum of likelihoods, i.e., cumulative probability, does not exceed a certain threshold \(p\), and then choose one of them randomly based on their probabilities (cf. below image; source).
 .
.
- Put simply, nucleus sampling, which has a hyperparameter top-\(p\), chooses from the smallest possible set of tokens whose summed probability (i.e., probability mass) exceeds top-\(p\) during decoding. Given this set of tokens, we re-normalize the probability distribution based on each token’s respective probability and then sample. Re-normalization involves adjusting these probabilities so they sum up to 1. This adjustment is necessary because the original probabilities were part of a larger set. After re-normalization, a new probability distribution is formed exclusively from this smaller, selected set of tokens, ensuring a fair sampling process within this subset. This is different from top-\(k\), which just samples from the $k$$ tokens with the highest probability.
Similar to top-\(k\) sampling, the choice between uniform and proportional selection in top-\(k\) sampling depends on the desired balance between diversity and coherence in the generated text. Uniform sampling promotes diversity by giving equal chance to all top \(k\) tokens, while proportional sampling favors coherence and contextual relevance by weighting tokens according to their probabilities. The specific application and user preference ultimately dictate the most suitable approach.
- The image below (source) illustrates how the algorithm works if \(p\) is 15% (i.e., top-\(p\) value of 0.15).

- In terms of practical usage, nucleus sampling can be controlled by setting the top-\(p\) parameter in most language model APIs (cf. GPT-3 API in Nucleus sampling v/s Temperature below).
How is nucleus sampling useful?
- Top-\(p\) is more suitable for tasks that require more fine-grained control over the diversity and fluency of the output, such as language modeling and text summarization. However, in reality, \(p\) is actually set a lot higher (about 75%) to limit the long tail of low probability tokens that may have been sampled.
- Furthermore, consider a case where a single token has a very high probability (i.e., larger than top-\(p\)). In this case, nucleus sampling will always sample this token. Alternatively, assigning more uniform probability across tokens may cause a larger number of tokens to be considered during decoding. Put simply, nucleus sampling can dynamically adjust the number of tokens that are considered during decoding based on their probabilities.
- Additionally top-\(k\) and top-\(p\) can work simultaneously, but \(p\) will always come after \(k\).
Greedy vs. top-\(k\) and top-\(p\)
- Deterministic vs. Stochastic: Greedy decoding is deterministic (always picks the highest probability token), while top-\(k\) and top-\(p\) are stochastic, introducing randomness into the selection process.
- Uniformity: In top-\(k\) sampling, once the top \(k\) tokens are selected, the choice among them can be uniform (each of the top \(k\) tokens has an equal chance of being picked) or proportional to their calculated probabilities.
- Bias: The method used can introduce a bias in the type of text generated. Greedy decoding tends to be safe and less creative, while stochastic methods can generate more novel and varied text (especially, using uniform sampling as explained earlier) but with a higher chance of producing irrelevant or nonsensical output.
Nucleus sampling v/s Temperature
- From the GPT-3 API below, we should only use either nucleus sampling or temperature, as APIs such as OpenAI say that these parameters cannot be used in tandem. Put simply, these are different and disjoint methods of controlling the randomness of a language model’s output.

References
- Hinton, Geoffrey, Oriol Vinyals, and Jeff Dean. “Distilling the knowledge in a neural network.” arXiv preprint arXiv:1503.02531 (2015)
- What is Temperature in LSTM (and neural networks generally)?
- Stanford CS224n
- Ketan Doshi’s Foundations of NLP Explained Visually: Beam Search, How it Works
- Cohere Top k and Top p
- HuggingFace: Constrained Beam Search