Primers • Transformers
- Background: Representation Learning for NLP
- Enter the Transformer
- Transformers vs. Recurrent and Convolutional Architectures: An Overview
- Breaking Down the Transformer
- Background
- One-Hot Encoding
- Dot product
- Matrix Multiplication as a Series of Dot Products
- First-Order Sequence Model
- Second-Order Sequence Model
- Second-Order Sequence Model with Skips
- Masking Features
- From Feature Vectors to Transformers
- Attention as Matrix Multiplication
- Second-Order Sequence Model as Matrix Multiplications
- Sampling a Sequence of Output Words
- Transformer Core
- Embeddings
- Positional Encoding
- Decoding Output Words / De-Embeddings
- Attention
- Why attention? Contextualized Word Embeddings
- Types of Attention: Additive, Multiplicative (Dot-product), and Scaled
- Attention calculation
- Self-Attention
- Single Head Attention Revisited
- Why is the product of the \(Q\) and \(K\) matrix in Self-Attention normalized?
- Coding up self-attention
- Averaging is equivalent to uniform attention
- Activation Functions
- Attention in Transformers: What’s new and what’s not?
- Calculating \(Q\), \(K\), and \(V\) matrices in the Transformer architecture
- Optimizing Performance with the KV Cache
- Applications of Attention in Transformers
- Multi-Head Attention
- Cross-Attention
- Dropout
- Skip connections
- Layer normalization
- Softmax
- Stacking Transformer Layers
- Transformer Encoder and Decoder
- Putting it all together: The Transformer Architecture
- Loss function
- Background
- Implementation details
- The relation between transformers and Graph Neural Networks
- Time complexity: RNNs vs. Transformers
- Lessons Learned
- Transformers: merging the worlds of linguistic theory and statistical NLP using fully connected graphs
- Long term dependencies
- Are Transformers learning neural syntax?
- Why multiple heads of attention? Why attention?
- Benefits of Transformers compared to RNNs/GRUs/LSTMs
- What would we like to fix about the transformer? / Drawbacks of Transformers
- Why is training Transformers so hard?
- Transformers: Extrapolation engines in high-dimensional space
- The road ahead for Transformers
- Choosing the right language model for your NLP use-case: key takeaways
- Transformers Learning Recipe
- Transformers From Scratch
- The Illustrated Transformer
- Lilian Weng’s The Transformer Family
- The Annotated Transformer
- Attention Is All You Need
- HuggingFace Encoder-Decoder Models
- Transformers library by HuggingFace
- Inference Arithmetic
- Transformer Taxonomy
- GPT in 60 Lines of NumPy
- x-transformers
- Speeding up the GPT - KV cache
- Transformer Poster
- FAQs
- Did the original Transformer use absolute or relative positional encoding?
- How does the choice of positional encoding method can influence the number of parameters added to the model? Consinder absolute, relative, and rotary positional encoding mechanisms.
- In Transformer-based models, why is RoPE required for context length extension?
- Why is the Transformer Architecture not as susceptible to vanishing gradients compared to RNNs?
- What is the fraction of attention weights relative to feed-forward weights in common LLMs?
- In BERT, how do we go from \(Q\), \(K\), and \(V\) at the final transformer block’s output to contextualized embeddings?
- What gets passed on from the output of the previous transformer block to the next in the encoder/decoder?
- In the vanilla transformer, what gets passed on from the output of the encoder to the decoder?
- Further Reading
- References
- Citation
Background: Representation Learning for NLP
- At a high level, all neural network architectures build representations of input data as vectors/embeddings, which encode useful syntactic and semantic information about the data. These latent or hidden representations can then be used for performing something useful, such as classifying an image or translating a sentence. The neural network learns to build better-and-better representations by receiving feedback, usually via error/loss functions.
- For Natural Language Processing (NLP), conventionally, Recurrent Neural Networks (RNNs) build representations of each word in a sentence in a sequential manner, i.e., one word at a time. Intuitively, we can imagine an RNN layer as a conveyor belt (as shown in the figure below; source), with the words being processed on it autoregressively from left to right. In the end, we get a hidden feature for each word in the sentence, which we pass to the next RNN layer or use for our NLP tasks of choice. Chris Olah’s legendary blog for recaps on LSTMs and representation learning for NLP is highly recommend to develop a background in this area
- Initially introduced for machine translation, Transformers have gradually replaced RNNs in mainstream NLP. The architecture takes a fresh approach to representation learning: Doing away with recurrence entirely, Transformers build features of each word using an attention mechanism (which had also been experimented in the world of RNNs as “Augmented RNNs”) to figure out how important all the other words in the sentence are w.r.t. to the aforementioned word. Knowing this, the word’s updated features are simply the sum of linear transformations of the features of all the words, weighted by their importance (as shown in the figure below; source). Back in 2017, this idea sounded very radical, because the NLP community was so used to the sequential–one-word-at-a-time–style of processing text with RNNs. As recommended reading, Lilian Weng’s Attention? Attention! offers a great overview on various attention types and their pros/cons.

Enter the Transformer
- History:
- LSTMs, GRUs and other flavors of RNNs were the essential building blocks of NLP models for two decades since 1990s.
- CNNs were the essential building blocks of vision (and some NLP) models for three decades since the 1980s.
- In 2017, Transformers (proposed in the “Attention Is All You Need” paper) demonstrated that recurrence and/or convolutions are not essential for building high-performance natural language models.
- In 2020, Vision Transformer (ViT) (An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale) demonstrated that convolutions are not essential for building high-performance vision models.
- The most advanced architectures in use before Transformers gained a foothold in the field were RNNs with LSTMs/GRUs. These architectures, however, suffered from the following drawbacks:
- They struggle with really long sequences (despite using LSTM and GRU units).
- They are fairly slow, as their sequential nature doesn’t allow any kind of parallel computing.
- At the time, LSTM-based recurrent models were the de-facto choice for language modeling. Here’s a timeline of some relevant events:
- ELMo (LSTM-based): 2018
- ULMFiT (LSTM-based): 2018
- Initially introduced for machine translation by Vaswani et al. (2017), the vanilla Transformer model utilizes an encoder-decoder architecture, which is able to perform sequence transduction with a sophisticated attention mechanism. As such, compared to prior recurrent architectures, Transformers possess fundamental differences in terms of how they work:
- They work on the entire sequence calculating attention across all word-pairs, which let them learn long-range dependencies.
- Some parts of the architecture can be processed in parallel, making training much faster.
- Owing to their unique self-attention mechanism, transformer models offer a great deal of representational capacity/expressive power.
- These performance and parallelization benefits led to Transformers gradually replacing RNNs in mainstream NLP. The architecture takes a fresh approach to representation learning: Doing away with recurrence entirely, Transformers build features of each word using an attention mechanism to figure out how important all the other words in the sentence are w.r.t. the aforementioned word. As such, the word’s updated features are simply the sum of linear transformations of the features of all the words, weighted by their importance.
- Back in 2017, this idea sounded very radical, because the NLP community was so used to the sequential – one-word-at-a-time – style of processing text with RNNs. The title of the paper probably added fuel to the fire! For a recap, Yannic Kilcher made an excellent video overview.
- However, Transformers did not become a overnight success until GPT and BERT immensely popularized them. Here’s a timeline of some relevant events:
- Attention is all you need: 2017
- Transformers revolutionizing the world of NLP, Speech, and Vision: 2018 onwards
- GPT (Transformer-based): 2018
- BERT (Transformer-based): 2018
- Today, transformers are not just limited to language tasks but are used in vision, speech, and so much more. The following plot (source) shows the transformers family tree with prevalent models:

- And, the plots below (first plot source); (second plot source) show the timeline for prevalent transformer models:


- Lastly, the plot below (source) shows the timeline vs. number of parameters for prevalent transformer models:

Transformers vs. Recurrent and Convolutional Architectures: An Overview
Language
- In a vanilla language model, for example, nearby words would first get grouped together. The transformer, by contrast, runs processes so that every element in the input data connects, or pays attention, to every other element. This is referred to as “self-attention.” This means that as soon as it starts training, the transformer can see traces of the entire data set.
- Before transformers came along, progress on AI language tasks largely lagged behind developments in other areas. Infact, in this deep learning revolution that happened in the past 10 years or so, natural language processing was a latecomer and NLP was, in a sense, behind computer vision, per the computer scientist Anna Rumshisky of the University of Massachusetts, Lowell.
- However, with the arrival of Transformers, the field of NLP has received a much-needed push and has churned model after model that have beat the state-of-the-art in various NLP tasks.
- As an example, to understand the difference between vanilla language models (based on say, a recurrent architecture such as RNNs, LSTMs or GRUs) vs. transformers, consider these sentences: “The owl spied a squirrel. It tried to grab it with its talons but only got the end of its tail.” The structure of the second sentence is confusing: What do those “it”s refer to? A vanilla language model that focuses only on the words immediately around the “it”s would struggle, but a transformer connecting every word to every other word could discern that the owl did the grabbing, and the squirrel lost part of its tail.
Vision
In CNNs, you start off being very local and slowly get a global perspective. A CNN recognizes an image pixel by pixel, identifying features like edges, corners, or lines by building its way up from the local to the global. But in transformers, owing to self-attention, even the very first attention layer models global contextual information, making connections between distant image locations (just as with language). If we model a CNN’s approach as starting at a single pixel and zooming out, a transformer slowly brings the whole fuzzy image into focus.
- CNNs work by repeatedly applying filters on local patches of the input data, generating local feature representations (or “feature maps”) and incrementally increase their receptive field and build up to global feature representations. It is because of convolutions that photo apps can organize your library by faces or tell an avocado apart from a cloud. Prior to the transformer architecture, CNNs were thus considered indispensable to vision tasks.
- With the Vision Transformer (ViT), the architecture of the model is nearly identical to that of the first transformer proposed in 2017, with only minor changes allowing it to analyze images instead of words. Since language tends to be discrete, a lot of adaptations were to discretize the input image to make transformers work with visual input. Exactly mimicing the language approach and performing self-attention on every pixel would be prohibitively expensive in computing time. Instead, ViT divides the larger image into square units, or patches (akin to tokens in NLP). The size is arbitrary, as the tokens could be made larger or smaller depending on the resolution of the original image (the default is 16x16 pixels). But by processing pixels in groups, and applying self-attention to each, the ViT could quickly churn through enormous training data sets, spitting out increasingly accurate classifications.
- In Do Vision Transformers See Like Convolutional Neural Networks?, Raghu et al. sought to understand how self-attention powers transformers in vision-based tasks.
Multimodal Tasks
- As discussed in the Enter the Transformer section, other architectures are “one trick ponies” while multimodal learning requires handling of modalities with different patterns within a streamlined architecture with a reasonably high relational inductive bias to even remotely reach human-like intelligence. In other words, we needs a single versatile architecture that seamlessly transitions between senses like reading/seeing, speaking, and listening.
- The potential to offer a universal architecture that can be adopted for multimodal tasks (that requires simultaneously handling multiple types of data, such as raw images, video and language) is something that makes the transformer architecture unique and popular.
- Because of the siloed approach with earlier architectures where each type of data had its own specialized model, this was a difficult task to accomplish. However, transformers offer an easy way to combine multiple input sources. For example, multimodal networks might power a system that reads a person’s lips in addition to listening to their voice using rich representations of both language and image information.
- By using cross-attention, where the query vector originates from one source and the key and value vectors come from another, transformers become highly effective for multimodal learning.
- The transformer thus offers be a big step toward achieving a kind of “convergence” for neural net architectures, resulting in a universal approach to processing data from multiple modalities.
Breaking Down the Transformer
- Prior to delving into the internal mechanisms of the Transformer architecture by examining each of its constituent components in detail, it is essential to first establish a foundational understanding of several underlying mathematical and conceptual constructs. These include, but are not limited to, one-hot vectors, the dot product, matrix multiplication, embedding generation, and the attention mechanism.
Background
One-Hot Encoding
Overview
-
Digital computers are inherently designed to process numerical data. However, in most real-world scenarios, the input data encountered is not naturally numerical. For instance, images are represented by pixel intensity values, and speech signals are modeled as oscillograms or spectrograms. Therefore, the initial step in preparing such data for computational models, especially machine learning algorithms, is to convert non-numeric inputs—such as text—into a numerical format that can be subjected to mathematical operations.
-
One-hot encoding is a method that transforms categorical variables into a format suitable for machine learning algorithms to enhance their predictive performance. Specifically, it converts categorical data into a binary matrix that enables the model to interpret each category as a distinct and independent feature.
Conceptual Intuition
- As one begins to work with machine learning models, the term “one-hot encoding” frequently arises. For example, in the scikit-learn documentation, one-hot encoding is described as a technique to “encode categorical integer features using a one-hot aka one-of-K scheme.” To elucidate this concept, let us consider a concrete example.
Example: Basic Dataset
- Consider the following illustrative dataset:
| CompanyName | CategoricalValue | Price |
|---|---|---|
| VW | 1 | 20000 |
| Acura | 2 | 10011 |
| Honda | 3 | 50000 |
| Honda | 3 | 10000 |
-
In this example, the column CategoricalValue represents a numerical label associated with each unique categorical entry (i.e., company names). If an additional company were to be included, it would be assigned the next incremental value, such as 4. Thus, as the number of distinct entries increases, so too does the range of the categorical labels.
-
It is important to note that the above table is a simplified representation. In practice, categorical values are typically indexed from 0 to \(N - 1\), where \(N\) is the number of distinct categories.
-
The assignment of categorical labels can be efficiently performed using the
LabelEncoderprovided by thesklearnlibrary. -
Returning to one-hot encoding: by adhering to the procedures outlined in the
sklearndocumentation and conducting minor data preprocessing, we can transform the previous dataset into the following format, wherein a value of1denotes presence and0denotes absence:
| VW | Acura | Honda | Price |
|---|---|---|---|
| 1 | 0 | 0 | 20000 |
| 0 | 1 | 0 | 10011 |
| 0 | 0 | 1 | 50000 |
| 0 | 0 | 1 | 10000 |
-
At this point, it is worth contemplating why mere label encoding might be insufficient when training machine learning models. Why is one-hot encoding preferred?
-
The limitation of label encoding lies in its implicit assumption of ordinal relationships among categories. For example, it inadvertently introduces a false hierarchy by implying
VW > Acura > Hondadue to their numeric encodings. If the model internally computes an average or distance metric over such values, the result could be misleading. Consider:(1 + 3)/2 = 2, which incorrectly suggests that the average of VW and Honda is Acura. Such outcomes undermine the model’s predictive accuracy and can lead to erroneous inferences. -
Therefore, one-hot encoding is employed to mitigate this issue. It effectively “binarizes” the categorical variable, enabling each category to be treated as an independent and mutually exclusive feature.
-
As a further example, suppose there exists a categorical feature named
flower, which can take the valuesdaffodil,lily, androse. One-hot encoding transforms this feature into three distinct binary features:is_daffodil,is_lily, andis_rose.
Example: Natural Language Processing (NLP)
-
Drawing inspiration from Brandon Rohrer’s “Transformers From Scratch”, let us consider another illustrative scenario within the domain of natural language processing. Imagine we are designing a machine translation system that converts textual commands from one language to another. Such a model would receive a sequence of sounds and produce a corresponding sequence of words.
-
The first step involves defining the vocabulary—the set of all symbols that may appear in any input or output sequence. For this task, we would require two separate vocabularies: one representing input sounds and the other for output words.
-
Assuming we are working in English, the vocabulary could easily span tens of thousands of words, with additional entries to capture domain-specific jargon. This would result in a vocabulary size approaching one hundred thousand.
-
One straightforward method to convert words to numbers is to assign each word a unique integer ID. For instance, if our vocabulary consists of only three words—
files,find, andmy—we might map them as follows:files = 1,find = 2, andmy = 3. The phrase “Find my files” then becomes the sequence[2, 3, 1]. -
While this method is valid, an alternative representation that is more computationally favorable is one-hot encoding. In this approach, each word is encoded as a binary vector of length equal to the vocabulary size, where all elements are
0except for a single1at the index corresponding to the word. -
In other words, each word is still assigned a unique number, but now this number serves as an index in a binary vector. Using our earlier vocabulary, the phrase “find my files” can be encoded as follows:

- Thus, the sentence becomes a sequence of one-dimensional arrays (i.e., vectors), which, when concatenated, forms a two-dimensional matrix:

- It is pertinent to note that in this primer and many other contexts, the terms “one-dimensional array” and “vector” are used interchangeably. Likewise, “two-dimensional array” and “matrix” may be treated synonymously.
Dot product
- One really useful thing about the one-hot representation is that it lets us compute dot product (also referred to as the inner product, scalar product or cosine similarity).
Algebraic Definition
-
The dot product of two vectors \(\mathbf{a}=\left[a_{1}, a_{2}, \ldots, a_{n}\right]\) and \(\mathbf{b}=\left[b_{1}, b_{2}, \ldots, b_{n}\right]\) is defined as:
\[\mathbf{a} \cdot \mathbf{b}=\sum_{i=1}^{n} a_{i} b_{i}=a_{1} b_{1}+a_{2} b_{2}+\cdots+a_{n} b_{n}\]- where \(\Sigma\) denotes summation and \(n\) is the dimension of the vector space.
-
For instance, in three-dimensional space, the dot product of vectors \([1, 3, -5]\) and \([4,-2,-1]\) is:
\[\begin{aligned} {[1,3,-5] \cdot[4,-2,-1] } &=(1 \times 4)+(3 \times-2)+(-5 \times-1) \\ &=4-6+5 \\ &=3 \end{aligned}\] -
The dot product can also be written as a product of two vectors, as below.
\[\mathbf{a} \cdot \mathbf{b}=\mathbf{a b}^{\top}\]- where \(\mathbf{b}^{\top}\) denotes the transpose of \(\mathbf{b}\).
-
Expressing the above example in this way, a \(1 \times 3\) matrix (row vector) is multiplied by a \(3 \times 1\) matrix (column vector) to get a \(1 \times 1\) matrix that is identified with its unique entry:
\[\left[\begin{array}{lll} 1 & 3 & -5 \end{array}\right]\left[\begin{array}{c} 4 \\ -2 \\ -1 \end{array}\right]=3\] -
Key takeaway:
- In summary, to get the dot product of two vectors, multiply their corresponding elements, then add the results. For a visual example of calculating the dot product for two vectors, check out the figure below.

Geometric Definition
-
In Euclidean space, a Euclidean vector is a geometric object that possesses both a magnitude and a direction. A vector can be pictured as an arrow. Its magnitude is its length, and its direction is the direction to which the arrow points. The magnitude of a vector a is denoted by \(\mid \mid a \mid \mid\). The dot product of two Euclidean vectors \(\mathbf{a}\) and \(\mathbf{b}\) is defined by,
\[\mathbf{a} \cdot \mathbf{b}=\|\mathbf{a}\|\|\mathbf{b}\| \cos \theta\]- where \(\theta\) is the angle between \(\mathbf{a}\) and \(\mathbf{b}\).
-
The above equation establishes the relation between dot product and cosine similarity.
Properties of the dot product
-
Dot products are especially useful when we’re working with our one-hot word representations owing to it’s properties, some of which are highlighted below.
-
The dot product of any one-hot vector with itself is one.

- The dot product of any one-hot vector with another one-hot vector is zero.

- The previous two examples show how dot products can be used to measure similarity. As another example, consider a vector of values that represents a combination of words with varying weights. A one-hot encoded word can be compared against it with the dot product to show how strongly that word is represented. The following figure shows how a similarity score between two vectors is calculated by way of calculating the dot product.

Matrix Multiplication as a Series of Dot Products
- The dot product constitutes the fundamental operation underlying matrix multiplication, which is a highly structured and well-defined procedure for combining two two-dimensional arrays (matrices). Let us denote the first matrix by \(A\) and the second by \(B\). In the most elementary scenario, where \(A\) consists of a single row and \(B\) consists of a single column, the matrix multiplication reduces to the dot product of these two vectors. This is illustrated in the figure below:

-
Observe that for this operation to be well-defined, the number of columns in matrix \(A\) must be equal to the number of rows in matrix \(B\). This dimensional compatibility is a prerequisite for the dot product to be computable.
-
As the dimensions of matrices \(A\) and \(B\) increase, the computational complexity of matrix multiplication grows accordingly—specifically, in a quadratic manner with respect to the matrix dimensions. When matrix \(A\) contains multiple rows, the multiplication proceeds by computing the dot product between each row of \(A\) and the entire matrix \(B\). Each such operation produces a single scalar value, and the collection of these values forms a resulting matrix with the same number of rows as \(A\). This process is depicted in the following figure, which shows the multiplication of a two-row matrix and a single-column matrix:

- If matrix \(B\) possesses more than one column, the operation is generalized by taking the dot product of each row in \(A\) with each column in \(B\). The outcome of each row-column dot product populates the corresponding cell in the resultant matrix. The figure below demonstrates the multiplication of a one-row matrix with a two-column matrix:

- Building on these principles, we can now define the general case of matrix multiplication for two arbitrary matrices, provided that the number of columns in matrix \(A\) equals the number of rows in matrix \(B\). The resultant matrix will have a shape defined by the number of rows in \(A\) and the number of columns in \(B\). This general case is visualized in the figure below, which illustrates the multiplication of a one-by-three matrix with a two-column matrix:

Matrix Multiplication as a Table Lookup
-
In the preceding section, we examined how matrix multiplication can function as a form of table lookup.
-
Consider a matrix \(A\) composed of a stack of one-hot encoded vectors. For the sake of illustration, suppose these vectors have non-zero entries (i.e., ones) located in the first column, fourth column, and third column, respectively. During matrix multiplication with another matrix \(B\), these one-hot vectors act as selection mechanisms that extract the corresponding rows—specifically, the first, fourth, and third rows—from matrix \(B\), in that order.
-
This method of employing a one-hot vector to selectively retrieve a specific row from a matrix lies at the conceptual foundation of the Transformer architecture. It enables discrete, deterministic access to embedding representations or other learned vector structures by treating the multiplication as a row-indexing operation.
First-Order Sequence Model
-
Let us momentarily set aside matrices and return our focus to sequences of words, which are the primary objects of interest in natural language processing.
-
Suppose we are developing a rudimentary natural language interface for a computer system, and initially, we aim to accommodate only three predefined command phrases:
Show me my directories please.
Show me my files please.
Show me my photos please.
- Given these sample utterances, our working vocabulary consists of the following seven distinct words:
{directories, files, me, my, photos, please, show}
-
One effective way to represent such sequences is through the use of a transition model, which encapsulates the probabilistic dependencies between successive words. For each word in the vocabulary, the model estimates the likelihood of possible subsequent words. For instance, if users refer to photos 50% of the time, files 30% of the time, and directories 20% of the time following the word “my”, these probabilities define a distribution over transitions from “my”.
-
Importantly, the transition probabilities originating from any given word must collectively sum to one, reflecting a complete probability distribution over the vocabulary. The following diagram illustrates this concept in the form of a Markov chain:

-
This specific type of transition model is referred to as a Markov chain, as it satisfies the Markov property: the probability of transitioning to the next word depends only on a limited number of prior states. More precisely, this is a first-order Markov model, meaning that the next word is conditioned only on the immediately preceding word. If the model instead considered the two most recent words, it would be categorized as a second-order Markov model.
-
We now return to matrices, which offer a convenient and compact representation of such probabilistic transition systems. The Markov chain can be encoded as a transition matrix, where each row and column corresponds to a unique word in the vocabulary, indexed identically to their respective positions in the one-hot encoding.
-
The transition matrix can thus be interpreted as a lookup table. Each row represents a starting word, and the values in that row’s columns indicate the probabilities of each word in the vocabulary occurring next. Because these values represent probabilities, they all lie in the interval \([0, 1]\), and the entries in each row collectively sum to 1.
-
The diagram below, adapted from Brandon Rohrer’s “Transformers From Scratch”, illustrates such a transition matrix:

-
Within this matrix, the structure of the three example sentences is clearly discernible. The vast majority of the transition probabilities are binary (i.e., either 0 or 1), indicating deterministic transitions. The only point of stochasticity arises after the word “my,” where the model branches probabilistically to either “directories,” “files,” or “photos.” Outside of this branching, the sequence progression is entirely deterministic, and this is reflected by the predominance of ones and zeros in the matrix.
-
We now revisit the earlier technique of matrix-vector multiplication for efficient retrieval. Specifically, we can multiply a one-hot vector—representing a given word—with the transition matrix to extract the associated row, which contains the conditional probability distribution for the next word. For example, to determine the distribution over words that follow “my,” we construct a one-hot vector for “my” and multiply it with the transition matrix. This operation retrieves the relevant row and thus reveals the desired transition probabilities.
-
The following figure, also from Brandon Rohrer’s “Transformers From Scratch”, visualizes this operation:

Second-Order Sequence Model
-
Predicting the next word in a sequence based solely on the current word is inherently limited. It is akin to attempting to predict the remainder of a musical composition after hearing only the initial note. The likelihood of accurate prediction improves significantly when at least two preceding words are taken into account.
-
This improvement is demonstrated using a simplified language model tailored for basic computer commands. Suppose the model is trained to recognize only the following two sentences, occurring in a \(\frac{40}{60}\) ratio, respectively:
Check whether the battery ran down please.
Check whether the program ran please.
- A first-order Markov chain—where the next word depends only on the immediately preceding word—can model this system. The diagram below, sourced from Brandon Rohrer’s Transformers From Scratch, illustrates the first-order transition structure:

-
However, this model exhibits limitations. If the model considers not just one but the two most recent words, its predictive accuracy improves. For instance, when it encounters the phrase
battery ran, it can confidently predict that the next word isdown. Conversely,program ranleads unambiguously toplease. Incorporating the second-most-recent word eliminates branching ambiguity, reduces uncertainty, and enhances model confidence. -
Such a system is known as a second-order Markov model, as it uses two previous states (words) to predict the next. While second-order chains are more difficult to visualize, the underlying connections offer greater predictive power. The diagram below, again from Brandon Rohrer’s Transformers From Scratch, illustrates this structure:

-
To emphasize the contrast, consider the following two transition matrices:
- First-order transition matrix:

- Second-order transition matrix:

-
In the second-order matrix, each row corresponds to a unique combination of two words, representing context for predicting the next word. Consequently, with a vocabulary size of \(N\), the matrix will contain \(N^2\) rows.
-
The advantage of this structure is increased certainty. The second-order matrix contains more entries with a value of 1 and fewer fractional probabilities, indicating a more deterministic model. Only a single row contains fractional values—highlighting the only point of uncertainty in the model. Intuitively, incorporating two words rather than one provides additional context, thereby enhancing the reliability of next-word predictions.
Second-Order Sequence Model with Skips
- A second-order model is effective when the word immediately following depends primarily on the two most recent words. However, complications arise when longer-range dependencies are necessary. Consider the following pair of equally likely sentences:
Check the program log and find out whether it ran please.
Check the battery log and find out whether it ran down please.
-
In this case, to accurately predict the word following
ran, one would need to reference context extending up to eight words into the past. One potential solution is to adopt a higher-order Markov model, such as a third-, fourth-, or even eighth-order model. However, this approach becomes computationally intractable: a naive implementation of an eighth-order model would necessitate a transition matrix with \(N^8\) rows, which is prohibitively large for realistic vocabulary sizes. -
An alternative strategy is to preserve a second-order model while allowing for non-contiguous dependencies. Specifically, the model considers the combination of the most recent word with any previously seen word in the sequence. Although each prediction still relies on just two words, the approach enables the model to capture long-range dependencies.
-
This technique, often termed second-order with skips, differs from full higher-order models in that it disregards much of the sequential ordering and only retains select pairwise interactions. Nevertheless, it remains effective for sequence modeling in many practical cases.
-
At this point, classical Markov chains are no longer applicable. Instead, the model tracks associative links between earlier words and subsequent words, regardless of strict temporal adjacency. The diagram below from Brandon Rohrer’s Transformers From Scratch visualizes these interactions using directional arrows. Numeric weights are omitted; instead, line thickness indicates the strength of association:

- The corresponding transition matrix for this second-order-with-skips model is shown below:

-
This matrix view is restricted to the rows pertinent to predicting the word that follows
ran. Each row corresponds to a pair consisting ofranand another word in the vocabulary. Only non-zero entries are shown; cells not displayed are implicitly zero. -
The first key insight is that, in this model, prediction is based not on a single row but on a collection of rows—each representing a feature defined by a specific word pair. Consequently, we move beyond traditional Markov chains. Rows no longer represent the complete state of a sequence, but instead denote individual contextual features active at a specific moment.
-
As a result of this shift, each value in the matrix is no longer interpreted as a probability, but rather as a vote. When predicting the next word, votes from all active features are aggregated, and the word receiving the highest cumulative score is selected.
-
The second key observation is that most features have little discriminatory power. Since the majority of words appear in both sentences, their presence does not help disambiguate what comes after
ran. These features contribute uniformly with a value of 0.5, offering no directional influence. -
The only features with predictive utility in this example are
battery, ranandprogram, ran. The featurebattery, ranimplies thatranis the most recent word andbatteryoccurred earlier. This feature assigns a vote of 1 todownand 0 toplease. Conversely,program, ranassigns the inverse: a vote of 1 topleaseand 0 todown. -
To generate a next-word prediction, the model sums all applicable feature values column-wise. For instance:
- In the sequence
Check the program log and find out whether it ran, the cumulative votes are 0 for most words, 4 fordown, and 5 forplease. - In the sequence
Check the battery log and find out whether it ran, the votes are reversed: 5 fordownand 4 forplease.
- In the sequence
-
By selecting the word with the highest vote total, the model makes the correct next-word prediction—even when the relevant information is located eight words earlier. This highlights the utility and efficiency of feature-based second-order-with-skips models in capturing long-range dependencies without incurring the exponential complexity of full higher-order Markov models.
Masking Features
-
Upon closer examination, the predictive difference between vote totals of 4 and 5 is relatively minor. Such a narrow margin indicates that the model lacks strong confidence in its prediction. In larger and more naturalistic language models, these subtle distinctions are likely to be obscured by statistical noise, potentially leading to inaccurate or unstable predictions.
-
One effective strategy to sharpen predictions is to eliminate the influence of uninformative features. In the given example, only two features—
battery, ranandprogram, ran—meaningfully contribute to next-word prediction. It is instructive at this point to recall that relevant rows are extracted from the transition matrix via a dot product between the matrix and a feature activity vector, which encodes the features currently active. For this scenario, the implicitly used feature vector is visualized in the following diagram from Brandon Rohrer’s Transformers From Scratch:

-
This vector includes an entry with the value 1 for each feature formed by pairing
ranwith each preceding word in the sentence. Notably, words that occur afterranare excluded, as in the next-word prediction task these words remain unseen at prediction time and therefore must not influence the outcome. Moreover, combinations that do not arise in the example context are safely assumed to yield zero values and can be ignored without loss of generality. -
To enhance model precision further, we can introduce a masking mechanism that explicitly nullifies unhelpful features. A mask is defined as a binary vector, populated with ones at positions corresponding to features we wish to retain, and zeros at positions to be suppressed or ignored. In this case, we wish to retain only
battery, ranandprogram, ran, the features that empirically prove to be informative. The masked feature vector is illustrated in the diagram below, also from Brandon Rohrer’s Transformers From Scratch:

-
The mask is applied to the original feature activity vector via element-wise multiplication. For any feature retained by the mask (i.e., mask value of 1), its corresponding activity remains unchanged. Conversely, features masked out (i.e., mask value of 0) are forcibly zeroed out, regardless of their original value.
-
The practical effect of the mask is that large portions of the transition matrix are suppressed. All feature combinations of
ranwith any word other thanbatteryorprogramare effectively removed from consideration. The resultant masked transition matrix is shown below:

-
Once uninformative features are masked out, the model’s predictive power becomes significantly stronger. For instance, when the word
batteryappears earlier in the sequence, the model now assigns a probability weight of 1 todownand 0 topleasefor the next word followingran. What was previously a 25% difference in weighting has now become an unambiguous selection, or informally, an “infinite percent” improvement in certainty. A similar confidence gain is observed when the wordprogramappears earlier, resulting in a decisive preference forplease. -
This process of selective masking is a core conceptual component of the attention mechanism, as referenced in the title of the original Transformer paper. While the simplified mechanism described here provides an intuitive foundation, the actual implementation of attention in Transformers is more sophisticated. For a comprehensive treatment, refer to the original paper.
Generally speaking, an attention function determines the relative importance (or “weight”) of different input elements in producing an output representation. In the specific case of scaled dot-product attention, which the Transformer architecture employs, the mechanism adopts the query-key-value paradigm from information retrieval. An attention function performs a mapping from a query and a set of key-value pairs to a single output. This output is computed as a weighted sum of the values, where each weight is derived from a compatibility function—also known as an alignment function, as introduced in Bahdanau et al. (2014)—which measures the similarity between the query and each key.
- This overview introduces the fundamental principles of attention. The specific computational details and extensions, including multi-head attention and positional encoding, are addressed in the dedicated section on Attention.
Origins of attention
- As mentioned above, the attention mechanism originally introduced in Bahdanau et al. (2015) served as a foundation upon which the self-attention mechanism in the Transformer paper was based on.
- The following slide from Stanford’s CS25 course shows how the attention mechanism was conceived and is a perfect illustration of why AI/ML is an empirical field, built on intuition.

From Feature Vectors to Transformers
-
The selective-second-order-with-skips model provides a valuable conceptual framework for understanding the operations of Transformer-based architectures, particularly on the decoder side. It serves as a reasonable first-order approximation of the underlying mechanics in generative language models such as OpenAI’s GPT-3. Although it does not fully encompass the complexity of Transformer models, it encapsulates the core intuition that drives them.
-
The subsequent sections aim to bridge the gap between this high-level conceptualization and the actual computational implementations of Transformers. The evolution from intuition to implementation is primarily shaped by three key practical considerations:
-
Computational efficiency of matrix multiplications Modern computers are exceptionally optimized for performing matrix multiplications. In fact, an entire industry has emerged around designing hardware tailored for this specific operation. Central Processing Units (CPUs) handle matrix multiplications effectively due to their ability to leverage multi-threading. Graphics Processing Units (GPUs), however, are even more efficient, as they contain hundreds or thousands of dedicated cores optimized for highly parallelized computations. Consequently, any algorithm or computation that can be reformulated as a matrix multiplication can be executed with remarkable speed and efficiency. This efficiency has led to the analogy: matrix multiplication is like a bullet train—if your data (or “baggage”) can be expressed in its format, it will reach its destination extremely quickly.
-
Differentiability of every computational step Thus far, our examples have involved manually defined transition probabilities and masking patterns—effectively, manually specified model parameters. In practical settings, however, these parameters must be learned from data using the process of backpropagation. For backpropagation to function, each computational operation in the network must be differentiable. This means that any infinitesimal change in a parameter must yield a corresponding, computable change in the model’s loss function—the measure of error between predictions and target outputs.
-
Gradient smoothness and conditioning The loss gradient, which comprises the set of all partial derivatives with respect to the model’s parameters, must exhibit smoothness and favorable conditioning to ensure effective optimization. A smooth gradient implies that small parameter updates result in proportionally small and consistent changes in loss—facilitating stable convergence. A well-conditioned gradient further ensures that no direction in the parameter space dominates excessively over others. To illustrate: if the loss surface were analogous to a geographic landscape, then a well-conditioned loss would resemble gently rolling hills (as in the classic Windows screensaver), whereas a poorly conditioned loss would resemble the steep, asymmetrical cliffs of the Grand Canyon. In the latter case, optimization algorithms would struggle to find a consistent update direction due to varying gradients depending on orientation.
-
-
If we consider the science of neural network architecture to be about designing differentiable building blocks, then the art lies in composing these blocks such that the gradient is smooth and approximately uniform in all directions—ensuring robust training dynamics.
Attention as Matrix Multiplication
-
While it is relatively straightforward to assign feature weights by counting co-occurrences of word pairs and subsequent words during training, attention masks are not as trivially derived. Until now, mask vectors have been assumed or manually specified. However, within the Transformer architecture, the process of discovering relevant masks must be both automated and differentiable.
-
Although it might seem intuitive to use a lookup table for this purpose, the design imperative in Transformers is to express all major operations as matrix multiplications, for the reasons discussed above.
-
We can adapt the earlier lookup mechanism by aggregating all possible mask vectors into a matrix, and using the one-hot representation of the current word to extract the appropriate mask vector. This procedure is depicted in the diagram below:

-
For visual clarity, the diagram illustrates only the specific mask vector being accessed, though the full matrix contains one mask vector for each vocabulary entry.
-
This leads us into alignment with the formal Transformer architecture as described in the original paper. The mechanism for retrieving a relevant mask via matrix operations corresponds to the \(QK^T\) term in the attention equation, which is introduced in more detail in the section on Single Head Attention Revisited:
-
In this formulation:
- The matrix \(Q\) (queries) encodes the features we are currently focusing on.
- The matrix \(K\) (keys) stores the collection of masking vectors (or more broadly, content to be attended to).
- Since the keys are stored in columns, but queries are row vectors, the keys must be transposed (denoted by the \(T\) operator) to enable appropriate dot-product alignment.
-
The resulting dot product between the query and each key vector yields a compatibility score. This score is then scaled by \(\sqrt{d_k}\) (to stabilize gradients during training), and passed through a softmax function to convert it into a probability distribution over the values. Finally, this distribution is used to compute a weighted sum of the value vectors in \(V\).
-
While we will revisit and refine this formulation in upcoming sections, this abstraction already demonstrates the core idea: attention as differentiable lookup, implemented entirely through matrix operations.
-
Additional elaboration on this mechanism can be found in the section on Attention below.
Second-Order Sequence Model as Matrix Multiplications
-
One aspect we have thus far treated somewhat informally is the construction of transition matrices. While the logical structure and function of these matrices have been discussed, we have not yet fully articulated how to implement them using matrix multiplication, which is central to efficient neural network computation.
-
Once the attention step is complete, it produces a vector that represents the most recent word along with a small subset of previously encountered words. This attention output provides the raw material necessary for feature construction, but it does not directly generate the multi-word (word-pair) features required for downstream processing. To construct these features—combinations of the most recent word with one or more earlier words—we can employ a single-layer fully connected neural network.
-
To illustrate how such a neural network layer can perform this construction, we will design a hand-crafted example. While this example is intentionally stylized and its weight values do not reflect real-world training outcomes, it serves to demonstrate that a neural network possesses the expressive capacity required to form word-pair features. For clarity and conciseness, we will restrict the vocabulary to just three attended words:
battery,program, andran. The following diagram from Brandon Rohrer’s Transformers From Scratch shows a neural network layer designed to generate multi-word features:

- The diagram illustrates how learned weights in the network can combine presence (indicated by a
1) and absence (indicated by a0) of words to produce a set of feature activations. This same transformation can also be expressed in matrix form. The following image depicts the weight matrix corresponding to this feature generation layer:

- Feature activations are computed by multiplying this weight matrix by a vector representing the current word context—that is, the presence or absence of each relevant word seen so far. The next diagram, also from Rohrer’s primer, illustrates this computation for the feature
battery, ran:

- In this instance, the vector has ones in the positions corresponding to
batteryandran, a zero forprogram, and a bias input fixed at one (a standard element in neural networks to allow shifting the activation). The result of the matrix multiplication yields a1for thebattery, ranfeature and-1forprogram, ran. This demonstrates how specific combinations of input activations result in distinct feature detections. The computation forprogram, ranproceeds analogously, as shown here:

-
The final step in constructing these features involves applying a Rectified Linear Unit (ReLU) nonlinearity. The ReLU function replaces any negative values with zero, effectively acting as a thresholding mechanism that retains only positive activations. This ensures that features are expressed in binary form—indicating presence with a
1and absence with a0. -
With these steps complete, we now have a matrix-multiplication-based procedure for generating multi-word features. Although we initially described these as consisting solely of the most recent word and one preceding word, a closer examination reveals that this method is more general. When the feature generation matrix is learned (rather than hard-coded), the model is capable of representing more complex structures, including:
- Three-word combinations, such as
battery, program, ran, if they occur frequently enough during training. - Co-occurrence patterns that ignore the most recent word, such as
battery, program.
- Three-word combinations, such as
-
Such capabilities reveal that the model is not strictly limited to a selective-second-order-with-skips formulation, as previously implied. Rather, the actual representational capacity of Transformers extends beyond this simplification, capturing more nuanced and flexible feature structures. This additional complexity illustrates that our earlier model was a useful abstraction, but not a complete one—and that abstraction will continue to evolve as we explore further layers of the architecture.
-
Once generated, the multi-word feature matrix is ready to undergo one final matrix multiplication: the application of the second-order sequence model with skips, as introduced earlier. Altogether, the following sequence of feedforward operations is applied after the attention mechanism:
- Feature creation via matrix multiplication
- Application of ReLU nonlinearity
- Transition matrix multiplication
-
These operations correspond to the Feed Forward block in the Transformer architecture. The following equation from the original paper expresses this process concisely in mathematical terms:

- In the architectural diagram below, also from the Transformer paper, these operations are grouped together under the label Feed Forward:

Sampling a Sequence of Output Words
Generating Words as a Probability Distribution over the Vocabulary
-
Up to this point, our discussion has focused primarily on the task of next-word prediction. To extend this into the generation of entire sequences, such as complete sentences or paragraphs, several additional components must be introduced. One critical element is the prompt—a segment of initial text that provides the Transformer with contextual information and a starting point for further generation. This prompt serves as an input to the decoder, which corresponds to the right-hand side of the model architecture (as labeled “Outputs (shifted right)” in conventional visualizations).
-
The selection and design of a prompt that elicits meaningful or interesting responses from the model is a specialized practice known as prompt engineering. This emerging field exemplifies a broader trend in artificial intelligence where human users adapt their inputs to support algorithmic behavior, rather than expecting models to adapt to arbitrary human instructions.
-
During sequence generation, the decoder is typically initialized with a special token such as
<START>, which acts as a signal to commence decoding. This token enables the decoder to begin leveraging the compressed representation of the source input, as derived from the encoder (explored further in the section on Cross-Attention). The following animation from Jay Alammar’s The Illustrated Transformer illustrates two key processes:- Parallel ingestion of tokens by the encoder, culminating in the construction of key and value matrices.
- The decoder generating its first output token (although the
<START>token itself is not shown in this particular animation).

-
Once the decoder receives an initial input—either a prompt or a start token—it performs a forward pass. The output of this pass is a sequence of predicted probability distributions, with one distribution corresponding to each token position in the output sequence.
-
The process of translating internal model representations into discrete words involves several steps:
- The output vector from the decoder is passed through a linear transformation (a fully connected layer).
- The result is a high-dimensional vector of logits—unnormalized scores representing each word in the vocabulary.
- A softmax function converts these scores into a probability distribution.
- A final word is selected from this distribution (e.g., by choosing the most probable word).
-
This de-embedding pipeline is depicted in the following visualization from Jay Alammar’s The Illustrated Transformer:

Role of the Final Linear and Softmax Layers
-
The linear layer is a standard fully connected neural layer that projects the decoder’s output vector into a logits vector—a vector whose dimensionality equals the size of the model’s output vocabulary.
-
For context, a typical NLP model may recognize approximately 40,000 distinct English words. Consequently, the logits vector would be 40,000-dimensional, with each element representing the unnormalized score of a corresponding word in the vocabulary.
-
These raw scores are then processed by the softmax layer, which transforms them into a probability distribution over the vocabulary. This transformation enforces two key constraints:
- All output values are in the interval \([0, 1]\).
- The values collectively sum to 1.0, satisfying the conditions of a probability distribution.
-
At each decoding step, the probability distribution specifies the model’s predictions for all possible next words. However, we are primarily interested in the distribution’s output at the final position of the current sequence, since earlier tokens are already known and fixed.
-
The word corresponding to the highest probability in the distribution is selected as the next token (further elaborated in the section on Greedy Decoding).
Greedy Decoding
-
Several strategies exist for selecting the next word from the predicted probability distribution. The most straightforward among them is greedy decoding, which involves choosing the word with the maximum probability at each step.
-
After selecting this word, it is appended to the input sequence and the updated sequence is re-fed into the decoder. This process repeats auto-regressively, generating one token at a time until a stopping criterion is met—typically, the generation of an
<EOS>(end-of-sequence) token or the production of a predefined number of tokens. -
The animation below from Jay Alammar’s The Illustrated Transformer demonstrates how the decoder recursively generates output tokens by ingesting previously generated tokens:

- One additional mechanism relevant to decoding—but not yet detailed—is the use of a specialized masking strategy to ensure that the model only attends to past tokens and not future ones. This constraint enforces causality in the generation process and is implemented via masked multi-head attention. The specifics of this masking mechanism are addressed later in the section on Single Head Attention Revisited.
Transformer Core
Embeddings
-
As described thus far, a naïve representation of the Transformer architecture quickly becomes computationally intractable. For example, with a vocabulary size \(N = 50{,}000\), a transition matrix encoding probabilities between all possible input word pairs and their corresponding next words would require a matrix with 50,000 columns and \(50{,}000^2 = 2.5 \times 10^9\) rows—amounting to over 100 trillion parameters. Such a configuration is impractically large, even given the capabilities of modern hardware accelerators.
-
The computational burden is not solely due to the matrix size. Constructing a stable and robust transition-based language model would necessitate a training corpus that illustrates every conceivable word sequence multiple times. This requirement would far exceed the size and diversity of even the most extensive language datasets.
-
Fortunately, these challenges are addressed through the use of embeddings.
-
In a one-hot encoding scheme, each word in the vocabulary is represented as a vector of length \(N\), with all elements set to zero except for a single
1in the position corresponding to the word. Consequently, this representation lies in an \(N\)-dimensional space, where each word occupies a unique position one unit away from the origin along one axis. A simplified visualization of such a high-dimensional structure is provided below:

- By contrast, an embedding maps each word from this high-dimensional space into a lower-dimensional continuous space. In the language of linear algebra, this operation is known as projection. The image above illustrates how words might be projected into a two-dimensional space for illustrative purposes. Instead of needing \(N\) elements to represent each word, only two numbers—\((x, y)\) coordinates—are needed. A hypothetical 2D embedding for a small vocabulary is shown below, along with coordinates for some sample words:

-
A well-constructed embedding clusters semantically or functionally similar words near one another in this reduced space. Consequently, models trained in the embedding space learn generalized patterns that can be applied across groups of related words. For instance, if the model learns a transformation applicable to one word, that knowledge implicitly extends to all neighboring words in the embedded space. This property not only reduces the total number of parameters required but also significantly decreases the amount of training data needed to achieve generalization.
-
The illustration highlights how meaningful groupings may emerge: domain-specific nouns such as
battery,log, andprogrammay cluster in one region; prepositions likedownandoutin another; and verbs such ascheck,find, andranmay lie closer to the center. Although actual embeddings are generally more abstract and less visually interpretable, the core principle holds: semantic similarity corresponds to spatial proximity in the embedding space. -
Embeddings enable a drastic reduction in the number of trainable parameters. However, reducing dimensionality comes with a trade-off: semantic fidelity may be lost if too few dimensions are used. Rich linguistic structures and nuanced relationships require adequate space for distinct concepts to remain non-overlapping. Thus, the choice of embedding dimensionality reflects a compromise between computational efficiency and model expressiveness.
-
The transformation from a one-hot vector to its corresponding position in the embedded space is implemented as a matrix multiplication—a foundational operation in linear algebra and neural network design. Specifically, starting from a one-hot vector of shape \(1 \times N\), the word is projected into a space of dimension \(d\) (e.g., \(d = 2\)) using a projection matrix of shape \(N \times d\). The following diagram from Brandon Rohrer’s Transformers From Scratch illustrates such a projection matrix:

-
In the example, a one-hot vector representing the word
batteryselects the corresponding row in the projection matrix. This row contains the coordinates ofbatteryin the lower-dimensional space. For clarity, all other zeros in the one-hot vector and unrelated rows of the projection matrix are omitted in the diagram. In practice, however, the projection matrix is dense, with each row encoding a learned vector representation for its associated vocabulary word. -
Projection matrices can transform the original collection of one-hot vectors into arbitrary configurations in any target dimensionality. The core challenge lies in learning a useful projection—one that clusters related words and separates unrelated ones sufficiently. High-quality pre-trained embeddings (e.g., Word2Vec, GloVe) are available for many common languages. Nevertheless, in Transformer models, these embeddings are typically learned jointly during training, allowing them to adapt dynamically to the task at hand.
-
The placement of the embedding layer within the Transformer architecture is shown in the following diagram from the original Transformer paper:

Positional Encoding
In contrast to recurrent and convolutional neural networks, the Transformer architecture does not explicitly model relative or absolute position information in its structure.
- Up to this point, positional information for words has been largely overlooked, particularly for any words preceding the most recent one. Positional encodings (also known as positional embeddings) address this limitation by embedding spatial information into the transformer, allowing the model to comprehend the order of tokens in a sequence.
- Positional encodings are a crucial component of transformer models, enabling them to understand the order of tokens in a sequence. Absolute positional encodings, while straightforward, are limited in their ability to generalize to different sequence lengths. Relative positional encodings address some of these issues but at the cost of increased complexity. Rotary Positional Encodings offer a promising middle ground, capturing relative positions efficiently and enabling the processing of very long sequences in modern LLMs. Each method has its strengths and weaknesses, and the choice of which to use depends on the specific requirements of the task and the model architecture.
Absolute Positional Encoding
- Definition and Purpose:
- Absolute positional encoding, proposed in the original Transformer paper Attention Is All You Need (2017) by Vaswani et al., is a method used in transformer models to incorporate positional information into the input sequences. Since transformers lack an inherent sense of order, positional encodings are essential for providing this sequential information. The most common method, introduced in the original transformer model by Vaswani et al. (2017), is to add a circular wiggle to the embedded representation of words using sinusoidal positional encodings.
- The position of a word in the embedding space acts as the center of a circle. A perturbation is added based on the word’s position in the sequence, causing a circular pattern as you move through the sequence. Words that are close to each other in the sequence have similar perturbations, while words that are far apart are perturbed in different directions.
- Circular Wiggle:
- The following diagram from Brandon Rohrer’s Transformers From Scratch illustrates how positional encoding introduces this circular wiggle:

- Since a circle is a two-dimensional figure, representing this circular wiggle requires modifying two dimensions of the embedding space. In higher-dimensional spaces (as is typical), the circular wiggle is repeated across all other pairs of dimensions, each with different angular frequencies. In some dimensions, the wiggle completes many rotations, while in others, it may only complete a fraction of a rotation. This combination of circular wiggles of different frequencies provides a robust representation of the absolute position of a word within the sequence.
- Formula: For a position \(pos\) and embedding dimension \(i\), the embedding vector can be defined as:
\(PE_{(pos, 2i)} = \sin\left(\frac{pos}{10000^{2i/d_{model}}}\right)\)
\(PE_{(pos, 2i+1)} = \cos\left(\frac{pos}{10000^{2i/d_{model}}}\right)\)
- where \(d_{model}\) is the dimensionality of the model.
- Architecture Diagram: The architecture diagram from the original Transformer paper highlights how positional encoding is generated and added to the embedded words:

Why sinusoidal positional embeddings work?
- Absolute/sinusoidal positional embeddings add position information into the mix in a way that doesn’t disrupt the learned relationships between words and attention. For a deeper dive into the math and implications, Amirhossein Kazemnejad’s positional encoding tutorial is recommended.
Limitations of Absolute Positional Encoding
- Lack of Flexibility: While absolute positional encodings encode each position with a unique vector, they are limited in that they do not naturally generalize to unseen positions or sequences longer than those encountered during training. This poses a challenge when processing sequences of varying lengths or very long sequences, as the embeddings for out-of-range positions are not learned.
- Example: Consider a transformer trained on sentences with a maximum length of 100 tokens. If the model encounters a sentence with 150 tokens during inference, the positional encodings for positions 101 to 150 would not be well-represented, potentially degrading the model’s performance on longer sequences.
Relative Positional Encoding
- Definition and Purpose:
- Relative positional encoding, proposed in Self-Attention with Relative Position Representations (2018) by Shaw et al., addresses the limitations of absolute positional encoding by encoding the relative positions between tokens rather than their absolute positions. In this approach, the focus is on the distance between tokens, allowing the model to handle sequences of varying lengths more effectively.
- Relative positional encodings can be integrated into the attention mechanism of transformers. Instead of adding a positional encoding to each token, the model learns embeddings for the relative distances between tokens and incorporates these into the attention scores.
-
Relative Positional Encoding for a Sequence of Length N: For a sequence of length \(N\), the relative positions between any two tokens range from \(-N+1\) to \(N-1\). This is because the relative position between the first token and the last token in the sequence is \(-(N-1)\), and the relative position between the last token and the first token is \(N-1\). Therefore, we need \(2N-1\) unique relative positional encoding vectors to cover all possible relative distances between tokens.
- Example: If \(N = 5\), the possible relative positions range from \(-4\) (last token relative to the first) to \(+4\) (first token relative to the last). Thus, we need 9 relative positional encodings corresponding to the relative positions: \(-4, -3, -2, -1, 0, +1, +2, +3, +4\).
Limitations of Relative Positional Encoding
- Complexity and Scalability: While relative positional encodings offer more flexibility than absolute embeddings, they introduce additional complexity. The attention mechanism needs to account for relative positions, which can increase computational overhead, particularly for long sequences.
- Example: In scenarios where sequences are extremely long (e.g., hundreds or thousands of tokens), the number of relative positional encodings required (\(2N-1\)) can become very large, potentially leading to increased memory usage and computation time. This can make the model slower and more resource-intensive to train and infer.
Rotary Positional Embeddings (RoPE)
- Definition and Purpose:
- Rotary Positional Embeddings (RoPE), proposed in RoFormer: Enhanced Transformer with Rotary Position Embedding (2021) by Su et al., are a more recent advancement in positional encoding, designed to capture the benefits of both absolute and relative positional embeddings while being parameter-efficient. RoPE encodes absolute positional information using a rotation matrix, which naturally incorporates explicit relative position dependency in the self-attention formulation.
- RoPE applies a rotation matrix to the token embeddings based on their positions, enabling the model to infer relative positions directly from the embeddings. The very ability of RoPE to capture relative positions while being parameter-efficient has been key in the development of very long-context LLMs, like GPT-4, which can handle sequences of thousands of tokens.
- Mathematical Formulation: Given a token embedding \(x\) and its position \(pos\), the RoPE mechanism applies a rotation matrix \(R(pos)\) to the embedding:
-
The rotation matrix \(R(pos)\) is constructed using sinusoidal functions, ensuring that the rotation angle increases with the position index.
-
Capturing Relative Positions: The key advantage of RoPE is that the inner product of two embeddings rotated by their respective positions encodes their relative position. This means that the model can infer the relative distance between tokens from their embeddings, allowing it to effectively process long sequences.
-
Example: Imagine a sequence with tokens A, B, and C at positions 1, 2, and 3, respectively. RoPE would rotate the embeddings of A, B, and C based on their positions. The model can then determine the relative positions between these tokens by examining the inner products of their rotated embeddings. This ability to capture relative positions while maintaining parameter efficiency has been crucial in the development of very long-context LLMs like GPT-4, which can handle sequences of thousands of tokens.
-
Further Reading: For a deeper dive into the mathematical details of RoPE, Rotary Embeddings: A Relative Revolution by Eleuther AI offers a comprehensive explanation.
Limitations of Rotary Positional Embeddings
- Specificity of the Mechanism: While RoPE is powerful and efficient, it is specifically designed for certain architectures and may not generalize as well to all transformer variants or other types of models. Moreover, its mathematical complexity might make it harder to implement and optimize compared to more straightforward positional encoding methods.
- Example: In practice, RoPE might be less effective in transformer models that are designed with very different architectures or in tasks where positional information is not as crucial. For instance, in some vision transformers where spatial positional encoding is more complex, RoPE might not offer the same advantages as in text-based transformers.
Decoding Output Words / De-Embeddings
-
While embedding words into a lower-dimensional continuous space significantly improves computational efficiency, at some point—particularly during inference or output generation—the model must convert these representations back into discrete tokens from the original vocabulary. This process, known as de-embedding, is conceptually and operationally analogous to embedding: it involves a projection from one vector space to another, implemented via matrix multiplication.
-
The de-embedding matrix shares the same structural form as the embedding matrix, but with the number of rows and columns transposed. Specifically:
- The number of rows corresponds to the dimensionality of the embedding space—for example, 2 in the toy example used throughout this discussion.
- The number of columns equals the size of the vocabulary, which, in our running example, is 13.
-
This projection operation maps the lower-dimensional embedded vector back into the high-dimensional vocabulary space. The following diagram illustrates the structure of the de-embedding transformation:

-
Although the numerical values within a trained de-embedding matrix are typically more difficult to visualize than those in an embedding matrix, the underlying mechanism is similar. When an embedded vector—say, one representing the word
program—is multiplied by the de-embedding matrix, the resulting value at the output position corresponding toprogramwill be relatively high. -
However, due to the nature of projections from a lower-dimensional space into a higher-dimensional one, the output vector will not exhibit a sparse structure. Specifically:
- Nearby words in the embedding space (i.e., those with similar vector representations) will also receive moderate to high values.
- Dissimilar or unrelated words will generally yield values close to zero.
- Additionally, negative values may appear, depending on the specific structure of the matrix and the input vector.
-
As a result, the output vector in the vocabulary space is dense—it contains mostly non-zero values and no longer resembles the one-hot vectors used for initial encoding. The following diagram illustrates such a representative dense result vector produced by de-embedding:

-
To convert this dense output back into a single discrete word, one common approach is to select the element with the highest value. This is referred to as the argmax operation, short for the “argument of the maximum.” The argmax returns the index (i.e., vocabulary word) associated with the maximum value in the output vector. This technique underlies greedy decoding, discussed previously in the section on sampling a sequence of output words. It serves as a strong baseline for sequence generation.
-
However, greedy decoding is not always optimal. If an embedded representation corresponds nearly equally well to multiple words, selecting only the highest-scoring one may sacrifice diversity and linguistic nuance. In such cases, always choosing the top prediction might result in repetitive or overly deterministic outputs.
-
Furthermore, more advanced sequence generation strategies—such as beam search or top-k sampling—require the model to evaluate multiple possible next tokens, sometimes several steps into the future, before committing to a final choice. To enable these strategies, the dense output vector from de-embedding must first be transformed into a probability distribution over the vocabulary.
Attention
- Now that we’ve made peace with the concepts of projections (matrix multiplications) and spaces (vector sizes), we can revisit the core attention mechanism with renewed vigor. It will help clarify the algorithm if we can be more specific about the shape of our matrices at each stage. There is a short list of important numbers for this.
- \(N\): vocabulary size; 13 in our example. Typically in the tens of thousands.
- \(n\): maximum sequence length; 12 in our example. Something like a few hundred in the paper (they don’t specify.) 2048 in GPT-3.
- \(d_{model}\): number of dimensions in the embedding space used throughout the model (512 in the paper).
- The original input matrix is constructed by getting each of the words from the sentence in their one-hot representation, and stacking them such that each of the one-hot vectors is its own row. The resulting input matrix has \(n\) rows and \(N\) columns, which we can abbreviate as \([n \times N]\).

- As we illustrated before, the embedding matrix has \(N\) rows and \(d_{model}\) columns, which we can abbreviate as \([N \times d_{model}]\). When multiplying two matrices, the result takes its number of rows from the first matrix, and its number of columns from the second. That gives the embedded word sequence matrix a shape of \([n \times d_{model}]\).
- We can follow the changes in matrix shape through the transformer as a way to track what’s going on (c.f. figure below; source). After the initial embedding, the positional encoding is additive, rather than a multiplication, so it doesn’t change the shape of things. Then the embedded word sequence goes into the attention layers, and comes out the other end in the same shape. (We’ll come back to the inner workings of these in a second.) Finally, the de-embedding restores the matrix to its original shape, offering a probability for every word in the vocabulary at every position in the sequence.

Why attention? Contextualized Word Embeddings
History
- Bag of words was the first technique invented to create a machine-representation of text. By counting the frequency of words in a piece of text, one could extract its “characteristics”. The following table (source) shows an example of the data samples (reviews) per row and the vocabulary of the model (unique words) across columns.

- However, this suggests that when all words are considered equally important, significant words like “crisis” which carry important meaning in the text can be drowned out by insignificant words like “and”, “for”, or “the” which add little information but are commonly used in all types of text.
- To address this issue, TF-IDF (Term Frequency-Inverse Document Frequency) assigns weights to each word based on its frequency across all documents. The more frequent the word is across all documents, the less weight it carries.
- However, this method is limited in that it treats each word independently and does not account for the fact that the meaning of a word is highly dependent on its context. As a result, it can be difficult to accurately capture the meaning of the text. This limitation was addressed with the use of deep learning techniques.
Enter Word2Vec: Neural Word Embeddings
- Word2Vec revolutionized embeddings by using a neural network to transform texts into vectors.
- Two popular approaches are the Continuous Bag of Words (CBOW) and Skip-gram models, which are trained using raw text data in an unsupervised manner. These models learn to predict the center word given context words or the context words given the center word, respectively. The resulting trained weights encode the meaning of each word relative to its context.
- The following figure (source) visualizes CBOW where the target word is predicted based on the context using a neural network:

- However, Word2Vec and similar techniques (such as GloVe, FastText, etc.) have their own limitations. After training, each word is assigned a unique embedding. Thus, polysemous words (i.e, words with multiple distinct meanings in different contexts) cannot be accurately encoded using this method. As an example:
“The man was accused of robbing a bank.” “The man went fishing by the bank of the river.”
- As another example:
“Time flies like an arrow.” “Fruit flies like a banana.”
- This limitation gave rise to contextualized word embeddings.
Contextualized Word Embeddings
- Transformers, owing to their self-attention mechanism, are able to encode a word using its context. This, in turn, offers the ability to learn contextualized word embeddings.
- Note that while Transformer-based architectures (e.g., BERT) learn contextualized word embeddings, prior work (ELMo) originally proposed this concept.
- As indicated in the prior section, contextualized word embeddings help distinguish between multiple meanings of the same word, in case of polysemous words.
- The process begins by encoding each word as an embedding (i.e., a vector that represents the word and that LLMs can operate with). A basic one is one-hot encoding, but we typically use embeddings that encode meaning (the Transformer architecture begins with a randomly-initialized
nn.Embeddinginstance that is learnt during the course of training). However, note that the embeddings at this stage are non-contextual, i.e., they are fixed per word and do not incorporate context surrounding the word. - As we will see in the section on Single Head Attention Revisited, self-attention transforms the embedding to a weighted combination of the embeddings of all the other words in the text. This represents the contextualized embedding that packs in the context surrounding the word.
- Considering the example of the word bank above, the embedding for bank in the first sentence would have contributions (and would thus be influenced significantly) from words like “accused”, “robbing”, etc. while the one in the second sentence would utilize the embeddings for “fishing”, “river”, etc. In case of the word flies, the embedding for flies in the first sentence will have contributions from words like “go”, “soars”, “pass”, “fast”, etc. while the one in the second sentence would depend on contributions from “insect”, “bug”, etc.
- The following figure (source) shows an example for the word flies, and computing the new embeddings involves a linear combination of the representations of the other words, with the weight being proportional to the relationship (say, similarity) of other words compared to the current word. In other words, the output is computed as a weighted sum of the values, where the weight assigned to each value is computed by a compatibility function of the query with the corresponding key (also called the “alignment” function in Bengio’s original paper that introduced attention in the context of neural networks).

Types of Attention: Additive, Multiplicative (Dot-product), and Scaled
- The Transformer is based on “scaled dot-product attention”.
- The two most commonly used attention functions are additive attention (proposed by Bahdanau et al. (2015) in Neural Machine Translation by Jointly Learning to Align and Translate), and dot-product (multiplicative) attention. The scaled dot-product attention proposed in the Transformer paper is identical to dot-product attention, except for the scaling factor of \(\frac{1}{\sqrt{d_{k}}}\). Additive attention computes the compatibility function using a feed-forward network with a single hidden layer. While the two are similar in theoretical complexity, dot-product attention is much faster and more space-efficient in practice, since it can be implemented using highly optimized matrix multiplication code.
- While for small values of \(d_{k}\) the two mechanisms perform similarly, additive attention outperforms dot product attention without scaling for larger values of \(d_{k}\) (Massive Exploration of Neural Machine Translation Architectures). We suspect that for large values of \(d_{k}\), the dot products grow large in magnitude, pushing the softmax function into regions where it has extremely small gradients (To illustrate why the dot products get large, assume that the components of \(q\) and \(k\) are independent random variables with mean 0 and variance 1. Then their dot product, \(q \cdot k=\sum_{i=1}^{d_{k}} q_{i} k_{i}\), has mean 0 and variance \(d_{k}\).). To counteract this effect, we scale the dot products by \(\frac{1}{\sqrt{d_{k}}}\).
Attention calculation
- Let’s develop an intuition about the architecture using the language of mathematical symbols and vectors.
-
We update the hidden feature \(h\) of the \(i^{th}\) word in a sentence \(\mathcal{S}\) from layer \(\ell\) to layer \(\ell+1\) as follows:
\[h_{i}^{\ell+1}=\text { Attention }\left(Q^{\ell} h_{i}^{\ell}, K^{\ell} h_{j}^{\ell}, V^{\ell} h_{j}^{\ell}\right)\]- i.e.,
- where \(j \in \mathcal{S}\) denotes the set of words in the sentence and \(Q^{\ell}, K^{\ell}, V^{\ell}\) are learnable linear weights (denoting the Query, Key and Value for the attention computation, respectively).
Intuition 1
- This section is aimed at understanding the underlying philosophy regarding how attention should be understood. The key point is to understand the rationale for employing three distinct vectors and to grasp the overarching objective of the entire attention mechanism.
-
Consider a scenario in which each token within a sequence must update its representation by incorporating relevant information from surrounding tokens, regardless of their proximity. Self-Attention provides a dynamic, learnable mechanism to facilitate this process. It begins by projecting each input token’s embedding into three distinct vectors:
- Query (Q): Represents the information the token seeks or is interested in. It can be thought of as the token formulating a question regarding the surrounding context.
- Key (K): Represents the information that the token offers or the types of queries it is capable of answering. It serves as a label or identifier of the token’s content.
- Value (V): Represents the actual content or substance of the token that will be conveyed if it is attended to. This constitutes the payload.
- The fundamental interaction occurs between the queries and the keys. For a given token’s query, the mechanism compares it against the keys of all tokens in the sequence through a scaled dot-product operation. This comparison produces a set of raw scores, indicating the relevance or compatibility between the query and each key. A higher score signifies that the key is highly pertinent to the query’s current information requirement.
- Subsequently, these raw scores are passed through a softmax function. This critical step normalizes the scores across all tokens, transforming them into a probability distribution that sums to one. These normalized scores serve as attention weights, determining the proportion of attention the query token allocates to each corresponding value token.
- Finally, a weighted sum of all Value vectors is computed, utilizing the attention weights obtained from the softmax operation. The outcome is an updated representation for the original Query token, blending information selectively from across the entire sequence based on learned relevance.
-
The true innovation of this mechanism lies in its adaptability. The attention weights are dynamically computed based on the specific input sequence and the learned Query, Key, and Value projection matrices. This enables the model to achieve:
- Token-Dependent Context: Different tokens can attend to various parts of the sequence depending on their unique role or informational needs.
- Input-Specific Routing: The attention patterns can vary significantly across different inputs, allowing flexible handling of syntax, semantics, and long-range dependencies.
- Focus: The model can learn to disregard irrelevant tokens by assigning them near-zero attention weights, thereby concentrating on the most important tokens.
Intuition 2
- From Eugene Yan’s Some Intuition on Attention and the Transformer blog, to build intuition around the concept of attention, let’s draw a parallel from a real life scenario and reason about the concept of key-value attention:
Imagine yourself in a library. You have a specific question (query). Books on the shelves have titles on their spines (keys) that suggest their content. You compare your question to these titles to decide how relevant each book is, and how much attention to give each book. Then, you get the information (value) from the relevant books to answer your question.
- We can understand the attention mechanism better through the following pipeline (source):

- Taking in the features of the word \(h_{i}^{\ell}\) and the set of other words in the sentence \({h_{j}^{\ell} \forall j \in \mathcal{S}}\), we compute the attention weights \(w_{i j}\) for each pair \((i, j)\) through the dot-product, followed by a softmax across all \(j\)’s.
- Finally, we produce the updated word feature \(h_{i}^{\ell+1}\) for word \(i\) by summing over all \({h_{j}^{\ell}}\)’s weighted by their corresponding \(w_{i j}\). Each word in the sentence parallelly undergoes the same pipeline to update its features.
- For more details on attention (including an overview of the various types and mathematical formulation of each), please refer the Attention primer.
Self-Attention
-
In self-attention, the input is modeled as three different components (or abstractions): the query, key, and value. These three components are derived from the same input sequence but are processed through different linear transformations to capture various relationships within the sequence.
- Query: Represents the element of the input sequence for which the attention score is being computed.
- Key: Represents the elements against which the query is compared to determine the attention score.
- Value: Represents the elements that are combined based on the attention scores to produce the output.
- Since the queries, keys, and values are all drawn from the same source, we refer to this as self-attention (we use “attention” and “self-attention” interchangeably in this primer). Self-attention forms the core component of Transformers. Also, given the use of the dot-product to ascertain similarity between the query and key vectors, the attention mechanism is also called dot-product self-attention.
- Note that one of the benefits of self-attention over recurrence is that it’s highly parallelizable. In other words, the attention mechanism is performed in parallel for each word in the sentence to obtain their updated features in one shot. This is a big advantage for Transformers over RNNs, which update features word-by-word. In other words, Transformer-based deep learning models don’t require sequential data to be processed in order, allowing for parallelization and reduced training time on GPUs compared to RNNs.
Single Head Attention Revisited
-
In a previous section, we explored a conceptual treatment of attention in Attention as Matrix Multiplication. While the actual implementation is more complex, the earlier intuition remains foundationally useful. In practice, however, the queries and keys are no longer easily interpretable because they are projected into learned subspaces unique to each attention head.
-
In our conceptual model, each row in the queries matrix corresponded directly to a word in the vocabulary, represented via one-hot encoding—each vector uniquely identifying a word. In contrast, within a Transformer, each query is a vector in an embedded space, meaning that it no longer represents a single word but instead occupies a region near other words of similar semantic or syntactic roles.
-
Accordingly, the actual attention mechanism no longer establishes relationships between discrete, individual words. Rather, each attention head learns to map query vectors to points in a shared embedded space. This mapping enables attention to operate over clusters of semantically or contextually similar words, thus allowing for generalization across word types that play analogous roles. In essence, attention becomes a mechanism for establishing relationships between word groups, not just specific tokens.
-
Understanding the attention mechanism is greatly facilitated by tracking the matrix dimensions through the computation pipeline (adapted from source):

-
Let us consider the attention calculation step-by-step:
-
Let \(Q\) and \(K\) be the query and key matrices, respectively. Both have shape \([n \times d_k]\), where:
- \(n\) is the number of tokens (sequence length),
- \(d_k\) is the dimensionality of the key/query vectors.
-
The attention scores are computed by the matrix multiplication \(QK^T\):
\[[n \times d_k] \cdot [d_k \times n] = [n \times n]\] -
This results in a square matrix of attention scores, where each row corresponds to a query and each column to a key. The \([n \times n]\) matrix expresses the relevance of each key to each query.
-
To ensure that the resulting values remain within a range conducive to stable training dynamics, each score is scaled by \(\frac{1}{\sqrt{d_k}}\). This mitigates the risk of excessively large dot products, which can cause the softmax function to saturate.
-
The softmax function is then applied to each row, converting scores into a probability distribution. This results in values that are non-negative, normalized across each row, and sharply peaked—approximating an argmax operation.
-
The attention matrix, now shaped \([n \times n]\), effectively assigns contextual weights to each position in the sequence, specifying how much each token should attend to every other token.
-
These weights are then applied to the values matrix \(V\) (also shaped \([n \times d_v]\)), producing a new representation of the input that emphasizes the most relevant parts of the sequence for each token.
-
The full attention mechanism is thus captured by the following expression:
\[\operatorname{Attention}(Q, K, V) = \operatorname{softmax} \left( \frac{QK^T}{\sqrt{d_k}} \right) V\]
-
The attention function maps a query and a set of key-value pairs to an output, where the query, keys, values, and output are all vectors. The output is computed as a weighted sum of the values, with weights determined by a compatibility function (also known as an alignment function) between the query and the keys. This paradigm was originally introduced in Bahdanau et al. (2014), a foundational paper on attention in neural networks.
-
A nontrivial aspect of this computation is that attention is calculated not just for the most recent word in the sequence, but simultaneously for every token in the input. This includes earlier words (whose output tokens have already been predicted) and future words (which have not yet been generated). While the attention scores for previous tokens are technically redundant at inference time, they are retained during training for completeness and symmetry. As for future tokens, although their predecessors have not yet been fixed, including them in the computation ensures consistent dimensions and allows indirect influence during training.
-
However, when generating text sequentially (i.e., auto-regressively), it is critical to prevent a token from accessing future information—doing so would violate causality and compromise the model’s predictive validity. To enforce this constraint, the Transformer applies a masking mechanism, implemented in the “Masked Multi-Head Attention” block.
-
The masking procedure is direct but effective: all attention weights corresponding to positions after the current token are forcibly set to negative infinity before the softmax is applied. This ensures that the softmax output for those positions becomes effectively zero, thereby preventing attention leakage into future tokens.
-
In The Annotated Transformer, which provides a highly instructive line-by-line Python implementation of the original paper, the mask matrix is visualized. Each row of the mask corresponds to a token in the sequence:
- The first row is allowed to attend to only the first token.
- The last row is allowed to attend to itself and all preceding tokens.
-
The mask is an \([n \times n]\) matrix and is not applied via matrix multiplication, but rather through element-wise operations. Specifically, disallowed entries are set to negative infinity, while allowed entries remain unchanged. The resulting masked attention matrix is then processed by the softmax function. The visualization below depicts such a mask matrix for a sequence completion task:

-
Another critical insight is that attention, while often understood as a relationship between words, is more accurately described as a relationship between positions in the sequence. The attention matrix of shape \([n \times n]\) specifies, for each token at position \(i\) (row), the degree of relevance or focus it places on token \(j\) (column). This shift in perspective—from token-to-token to position-to-position—simplifies the mathematical formulation and enhances interpretability, especially when working in the abstract embedding space.
-
Thus, attention operates not on discrete vocabulary entries but on embedded vector representations of words. The soft alignment between positions allows the model to dynamically determine which parts of the sequence are most relevant for predicting the next token, while maintaining the temporal and semantic structure of the input.
Why is the product of the \(Q\) and \(K\) matrix in Self-Attention normalized?
- Let’s break down the reasoning behind normalizing the dot product of \(Q\) and \(K\) by the square root of the dimension of the keys.
Understanding the Role of \(Q\) and \(K\) in Self-Attention
-
In self-attention, each input token is associated with three vectors: the Query (\(Q\)), the Key (\(K\)), and the Value (\(V\)):
- Query (\(Q\)): Represents the current token for which we are computing the attention score. It is essentially asking, “To which other tokens should I pay attention?”
- Key (\(K\)): Represents each of the tokens that can be attended to. It acts as the potential target of attention, answering the question, “How relevant am I to a given query?”
- Value (\(V\)): Contains the actual information or feature vectors to be aggregated based on the attention scores.
Dot Product of \(Q\) and \(K\)
- To compute the attention score between a query and a key, we perform a dot product between the query vector \(q_i\) and each key vector \(k_j\):
- The result of this dot product gives us a measure of similarity or relevance between the current token (represented by the query) and another token (represented by the key). High dot product values indicate a high degree of similarity or relevance, suggesting that the model should pay more attention to this token.
Need for Normalization
-
Without normalization, the dot product values can become very large, especially when the dimensionality of the query and key vectors (\(d_k\)) is high. This is due to the following reasons:
- Magnitude Dependency: The dot product value is dependent on the dimensionality of the vectors. As the dimensionality increases, the magnitude of the dot product can also increase significantly, leading to a wider range of possible values.
- Gradient Instability: Large values in the dot product can cause the softmax function, which is used to convert attention scores into probabilities, to saturate. When the input values to softmax are large, it can result in a gradient that is too small, slowing down the learning process or causing vanishing gradient problems.
- Training Stability: Large variance in the attention scores can cause instability during training. If the scores are too large, the model’s output can become overly sensitive to small changes in input, making it difficult to learn effectively.
Normalization by Square Root of \(d_k\)
- To mitigate these issues, the dot product is scaled by the square root of the dimensionality of the key vectors (\(\sqrt{d_k}\)):
-
Here’s why this specific form of normalization is effective:
-
Variance Control: By scaling the dot product by \(\sqrt{d_k}\), we ensure that the variance of the dot product remains approximately constant and doesn’t grow with the dimensionality. This keeps the distribution of attention scores stable, preventing any single score from dominating due to large values.
-
Balanced Softmax Output: The scaling keeps the range of attention scores in a region where the softmax function can operate effectively. It prevents the softmax from becoming too peaked or too flat, ensuring that attention is distributed appropriately among different tokens.
-
Intuitive Interpretation
- The normalization can be interpreted as adjusting the scale of the dot product to make it invariant to the dimensionality of the vectors. Without this adjustment, as the dimensionality of the vectors increases, the dot product’s expected value would increase, making it harder to interpret the similarity between query and key. Scaling by \(\sqrt{d_k}\) effectively counteracts this growth, maintaining a stable range of similarity measures.
Conclusion
-
In summary, the normalization of the product of the \(Q\) and \(K\) matrices in self-attention is essential for:
- Controlling the variance of the attention scores.
- Ensuring stable and efficient training.
- Keeping the attention distribution interpretable and effective.
-
This scaling step is a simple yet crucial modification that significantly improves the performance and stability of self-attention mechanisms in models like Transformers.
Putting it all together
- The following infographic (source) provides a quick overview of the constituent steps to calculate attention.

- As indicated in the section on Contextualized Word Embeddings, Attention enables contextualized word embeddings by allowing the model to selectively focus on different parts of the input sequence when making predictions. Put simply, the attention mechanism allows the transformer to dynamically weigh the importance of different parts of the input sequence based on the current task and context.
- In an attention-based model like the transformer, the word embeddings are combined with attention weights that are learned during training. These weights indicate how much attention should be given to each word in the input sequence when making predictions. By dynamically adjusting the attention weights, the model can focus on different parts of the input sequence and better capture the context in which a word appears. As the paper states, the attention mechanism is what has revolutionized Transformers to what we see them to be today.
- Upon encoding a word as an embedding vector, we can also encode the position of that word in the input sentence as a vector (positional embeddings), and add it to the word embedding. This way, the same word at a different position in a sentence is encoded differently.
- The attention mechanism works with the inclusion of three vectors: key, query, value. Attention is the mapping between a query and a set of key-value pairs to an output. We start off by taking a dot product of query and key vectors to understand how similar they are. Next, the Softmax function is used to normalize the similarities of the resulting query-key vectors. The output is computed as a weighted sum of the values, where the weight assigned to each value is computed by a compatibility function of the query with the corresponding key.
- Thus, the basis behind the concept of attention is: “How much attention a word should pay to another word in the input to understand the meaning of the sentence?”
- As indicated in the section on Attention Calculation, one of the benefits of self-attention over recurrence is that it’s highly parallelizable. In other words, the attention mechanism is performed in parallel for each word in the sentence to obtain their updated features in one shot. Furthermore, learning long-term/long-range dependencies in sequences is another benefit.
- The architecture diagram from the original Transformer paper highlights the self-attention layer (in multi-head form in both the encoder (unmasked variant) and decoder (masked variant):

Coding up self-attention
Single Input
- To ensure that the matrix multiplications in the scaled dot-product attention function are valid, we need to add assertions to check the shapes of \(Q\), \(K\), and \(V\). Specifically, after transposing \(K\), the last dimension of \(Q\) should match the first dimension of \(K^T\) for the multiplication \(Q * K^T\) to be valid. Similarly, for the multiplication of the attention weights and \(V\), the last dimension of the attention weights should match the first dimension of \(V\).
- Here’s the updated code with these assertions:
import numpy as np
from scipy.special import softmax
def scaled_dot_product_attention_single(Q: np.ndarray, K: np.ndarray, V: np.ndarray) -> np.ndarray:
"""
Implements scaled dot-product attention for a single input using NumPy.
Includes shape assertions for valid matrix multiplications.
Parameters:
Q (np.ndarray): Query array of shape [seq_len, d_q].
K (np.ndarray): Key array of shape [seq_len, d_k].
V (np.ndarray): Value array of shape [seq_len, d_v].
Returns:
np.ndarray: Output array of the attention mechanism.
"""
# Ensure the last dimension of Q matches the first dimension of K^T
assert Q.shape[-1] == K.shape[-1], "The last dimension of Q must match the first dimension of K^T"
# Ensure the last dimension of attention weights matches the first dimension of V
assert K.shape[0] == V.shape[0], "The last dimension of K must match the first dimension of V"
d_k = Q.shape[-1] # Dimension of the key vectors
# Calculate dot products of Q with K^T and scale
scores = np.matmul(Q, K^T) / np.sqrt(d_k)
# Apply softmax to get attention weights
attn_weights = softmax(scores, axis=-1)
# Multiply by V to get output
output = np.matmul(attn_weights, V)
return output
# Test with sample input
def test_with_sample_input():
# Sample inputs
Q = np.array([[1, 0], [0, 1]])
K = np.array([[1, 0], [0, 1]])
V = np.array([[1, 2], [3, 4]])
# Function output
output = scaled_dot_product_attention_single(Q, K, V)
# Manually calculate expected output
d_k = Q.shape[-1]
scores = np.matmul(Q, K^T) / np.sqrt(d_k)
attn_weights = softmax(scores, axis=-1)
expected_output = np.matmul(attn_weights, V)
- Explanation:
- Two assertions are added:
- \(Q\) and \(K^T\) Multiplication: Checks that the last dimension of \(Q\) matches the first dimension of \(K^T\) (or the last dimension of \(K\)).
- Attention Weights and \(V\) Multiplication: Ensures that the last dimension of \(K\) (or \(K^T\)) matches the first dimension of \(V\), as the shape of the attention weights will align with the shape of \(K^T\) after softmax.
- Note that these shape checks are critical for the correctness of matrix multiplications involved in the attention mechanism. By adding these assertions, we ensure the function handles inputs with appropriate dimensions, avoiding runtime errors due to invalid matrix multiplications.
- Two assertions are added:
Batch Input
- In the batched version, the inputs \(Q\), \(K\), and \(V\) will have shapes
[batch_size, seq_len, feature_size]. The function then needs to perform operations on each item in the batch independently.
import numpy as np
from scipy.special import softmax
def scaled_dot_product_attention_batch(Q: np.ndarray, K: np.ndarray, V: np.ndarray) -> np.ndarray:
"""
Implements scaled dot-product attention for batch input using NumPy.
Includes shape assertions for valid matrix multiplications.
Parameters:
Q (np.ndarray): Query array of shape [batch_size, seq_len, d_q].
K (np.ndarray): Key array of shape [batch_size, seq_len, d_k].
V (np.ndarray): Value array of shape [batch_size, seq_len, d_v].
Returns:
np.ndarray: Output array of the attention mechanism.
"""
# Ensure batch dimensions of Q, K, V match
assert Q.shape[0] == K.shape[0] == V.shape[0], "Batch dimensions of Q, K, V must match"
# Ensure the last dimension of Q matches the last dimension of K
assert Q.shape[-1] == K.shape[-1], "The last dimension of Q must match the last dimension of K"
# Ensure the last dimension of K matches the last dimension of V
assert K.shape[1] == V.shape[1], "The first dimension of K must match the first dimension of V"
d_k = Q.shape[-1]
# Calculate dot products of Q with K^T for each batch and scale
scores = np.matmul(Q, K.transpose(0, 2, 1)) / np.sqrt(d_k)
# Apply softmax to get attention weights for each batch
attn_weights = softmax(scores, axis=-1)
# Multiply by V to get output for each batch
output = np.matmul(attn_weights, V)
return output
# Example test case for batched input
def test_with_batch_input():
batch_size, seq_len, feature_size = 2, 3, 4
Q_batch = np.random.randn(batch_size, seq_len, feature_size)
K_batch = np.random.randn(batch_size, seq_len, feature_size)
V_batch = np.random.randn(batch_size, seq_len, feature_size)
output = scaled_dot_product_attention_batch(Q_batch, K_batch, V_batch)
assert output.shape == (batch_size, seq_len, feature_size), "Output shape is incorrect for batched input"
- Explanation:
- The function now expects inputs with an additional batch dimension at the beginning.
- The shape assertions are updated to ensure that the batch dimensions of \(Q\), \(K\), and \(V\) match, and the feature dimensions are compatible for matrix multiplication.
- Matrix multiplications (
np.matmul) and the softmax operation are performed independently for each item in the batch. - The test case
test_with_batch_inputdemonstrates how to use the function with batched input and checks if the output shape is correct.
Averaging is equivalent to uniform attention
- On a side note, it is worthwhile noting that the averaging operation is equivalent to uniform attention with the weights being all equal to \(\frac{1}{n}\), where \(n\) is the number of words in the input sequence. In other words, averaging is simply a special case of attention.
Activation Functions
- The transformer does not use an activation function following the multi-head attention layer, but does use the ReLU activation sandwiched between the two position-wise fully-connected layers that form the feed-forward network. Put simply, the a fully connected feed-forward network in the transformer blocks consists of two linear transformations with a ReLU activation in between.
- The reason behind this goes back to the purpose of self-attention. The measure between word-vectors is generally computed through cosine-similarity because in the dimensions word tokens exist, it’s highly unlikely for two words to be collinear even if they are trained to be closer in value if they are similar. However, two trained tokens will have higher cosine-similarity if they are semantically closer to each other than two completely unrelated words.
- This fact is exploited by the self-attention mechanism; after several of these matrix multiplications, the dissimilar words will zero out or become negative due to the dot product between them, and the similar words will stand out in the resulting matrix.
- Thus, self-attention can be viewed as a weighted average, where less similar words become averaged out faster (toward the zero vector, on average), thereby achieving groupings of important and unimportant words (i.e. attention). The weighting happens through the dot product. If input vectors were normalized, the weights would be exactly the cosine similarities.
- The important thing to take into consideration is that within the self-attention mechanism, there are no inherent parameters; those linear operations are just there to capture the relationship between the different vectors by using the properties of the vectors used to represent them, leading to attention weights.
Attention in Transformers: What’s new and what’s not?
- The seq2seq encoder-decoder architecture that Vaswani et al. used is an idea adopted from one of Bengio’s papers, Neural Machine Translation by Jointly Learning to Align and Translate.
- Further, Transformers use scaled dot-product attention (based on Query, Key and Value matrices) which is a concept inspired from the field of information retrieval (note that Bengio’s seq2seq architecture group used Bahdanau attention in Neural Machine Translation by Jointly Learning to Align and Translate which is a more relatively basic form of attention compared to what Transformers use).
- However, what’s novel about Transformers is that Vaswani et al. applied attention to the encoder as well (along with applying (cross-)attention at the decoder, similar to how Bengio’s group did it in Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation – thereby leading to the concept of “self-attention”, which is unique to Transformers.
Calculating \(Q\), \(K\), and \(V\) matrices in the Transformer architecture
- Each word is embedded into a vector of size 512 and is fed into the bottom-most encoder. The abstraction that is common to all the encoders is that they receive a list of vectors each of the size 512 – in the bottom encoder that would be the word embeddings, but in other encoders, it would be the output of the encoder that is directly below. The size of this list is hyperparameter we can set – basically it would be the length of the longest sentence in our training dataset.
- In the self-attention layers, multiplying the input vector (which is the word embedding for the first block of the encoder/decoder stack, while the output of the previous block for subsequent blocks) by the attention weights matrix (which are the \(Q\), \(K\), and \(V\) matrices stacked horizontally) and adding a bias vector afterwards results in a concatenated key, value, and query vector for this token. This long vector is split to form the \(q\), \(k\), and \(v\) vectors for this token (which actually represent the concatenated output for multiple attention heads and is thus, further reshaped into \(q\), \(k\), and \(v\) outputs for each attention head — more on this in the section on Multi-head Attention). From Jay Alammar’s: The Illustrated GPT-2:

Optimizing Performance with the KV Cache
- Using a KV cache is one of the most commonly used tricks for speeding up inference with Transformer-based models, particularly employed with LLMs. Let’s unveil its inner workings.
- Autoregressive decoding process: When we perform inference with an LLM, it follows an autoregressive decoding process. Put simply, this means that we (i) start with a sequence of textual tokens, (ii) predict the next token, (iii) add this token to our input, and (iv) repeat until generation is finished.
- Causal self-attention: Self-attention within a language model is causal, meaning that each token only considers itself and prior tokens when computing its representation (i.e., NOT future tokens). As such, representations for each token do not change during autoregressive decoding! We need to compute the representation for each new token, but other tokens remain fixed (i.e., because they don’t depend on tokens that follow them).
- Caching self-attention values: When we perform self-attention, we project our sequence of tokens using three separate, linear projections: key projection, value projection, and query projection. Then, we execute self-attention using the resulting matrices. The KV-cache simply stores the results of the key and value projections for future decoding iterations so that we don’t recompute them every time!
- Why not cache the query? So why are the key and value projections cached, but not the query? This is simply because the entries in the query matrix are only needed to compute the representations of prior tokens in the sequence (whose key and value representations are already stored in the KV-Cache). At each time-step, the new query input consists of the token at that time-step and all prior tokens (i.e., the entire sequence up to that point). For computing the representation of query representation for the most recent token, we only need access to the most recent row in the query matrix.
- Updates to the KV cache: Throughout autoregressive decoding, we have the key and value projections cached. Each time we get a new token in our input, we simply compute the new rows as part of self-attention and add them to the KV cache. Then, we can use the query projection for the new token and the updated key and value projections to perform the rest of the forward pass.
- Latency optimization: KV-caching decreases the latency to the next token in an autoregressive setting starting from the second token. Since the prompt tokens are not cached at the beginning of the generation, time to the first token is high, but as KV-caching kicks in for further generation, latency reduces. In other words, KV-caching is the reason why the latency of the first token’s generation (from the time the input prompt is fed in) is higher than that of consecutive tokens.
- Scaling to Multi-head Self-attention: Here, we have considered single-head self-attention for simplicity. However, it’s important to note that the same exact process applies to the multi-head self-attention used by LLMs (detailed in the Multi-Head Attention section below). We just perform the exact same process in parallel across multiple attention heads.

- More on the KV cache in the Model Acceleration primer.
Applications of Attention in Transformers
- From the paper, the Transformer uses multi-head attention in three different ways:
- The encoder contains self-attention layers. In a self-attention layer, all of the keys, values, and queries are derived from the same source, which is the word embedding for the first block of the encoder stack, while the output of the previous block for subsequent blocks. Each position in the encoder can attend to all positions in the previous block of the encoder.
- Similarly, self-attention layers in the decoder allow each position in the decoder to attend to all positions in the decoder up to and including that position. We need to prevent leftward information flow in the decoder to preserve the auto-regressive property. We implement this inside of scaled dot-product attention by masking out all values (by setting to a very low value, such as \(−\infty\)) in the input of the softmax which correspond to illegal connections.
- In “encoder-decoder attention” layers, the queries come from the previous decoder layer, and the memory keys and values come from the output of the encoder. This allows every position in the decoder to attend over all positions in the input sequence. This mimics the typical encoder-decoder attention mechanisms in sequence-to-sequence models such as Neural Machine Translation by Jointly Learning to Align and Translate, Google’s neural machine translation system: Bridging the gap between human and machine translation, and Convolutional Sequence to Sequence Learning.
Multi-Head Attention
- Let’s confront some of the simplistic assumptions we made during our first pass through explaining the attention mechanism. Words are represented as dense embedded vectors, rather than one-hot vectors. Attention isn’t just 1 or 0, on or off, but can also be anywhere in between. To get the results to fall between 0 and 1, we use the softmax trick again. It has the dual benefit of forcing all the values to lie in our [0, 1] attention range, and it helps to emphasize the highest value, while aggressively squashing the smallest. It’s the differential almost-argmax behavior we took advantage of before when interpreting the final output of the model.
- An complicating consequence of putting a softmax function in attention is that it will tend to focus on a single element. This is a limitation we didn’t have before. Sometimes it’s useful to keep several of the preceding words in mind when predicting the next, and the softmax just robbed us of that. This is a problem for the model.
- To address the above issues, the Transformer paper refined the self-attention layer by adding a mechanism called “multi-head” attention. This improves the performance of the attention layer in two ways:
- It expands the model’s ability to focus on different positions. It would be useful if we’re translating a sentence like “The animal didn’t cross the street because it was too tired”, we would want to know which word “it” refers to.
- It gives the attention layer multiple “representation subspaces”. As we’ll see next, with multi-head attention we have not only one, but multiple sets of \(Q, K, V\) weight matrices (the Transformer uses eight attention heads, so we end up with eight sets for each encoder/decoder). Each of these sets is randomly initialized. Then, after training, each set is used to project the input embeddings (or vectors from lower encoders/decoders) into a different representation subspace.
- Further, getting the straightforward dot-product attention mechanism to work can be tricky. Bad random initializations of the learnable weights can de-stabilize the training process.
- Multiple heads lets the the transformer consider several previous words simultaneously when predicting the next. It brings back the power we had before we pulled the softmax into the picture.
- To fix the aforementioned issues, we can run multiple ‘heads’ of attention in parallel and concatenate the result (with each head now having separate learnable weights).
- To accomplish multi-head attention, self-attention is simply conducted multiple times on different parts of the \(Q, K, V\) matrices (each part corresponding to each attention head). Each \(q\), \(k\), and \(v\) vector generated at the output contains concatenated output corresponding to contains each attention head. To obtain the output corresponding to each attention heads, we simply reshape the long \(q\), \(k\), and \(v\) self-attention vectors into a matrix (with each row corresponding to the output of each attention head). From Jay Alammar’s: The Illustrated GPT-2:
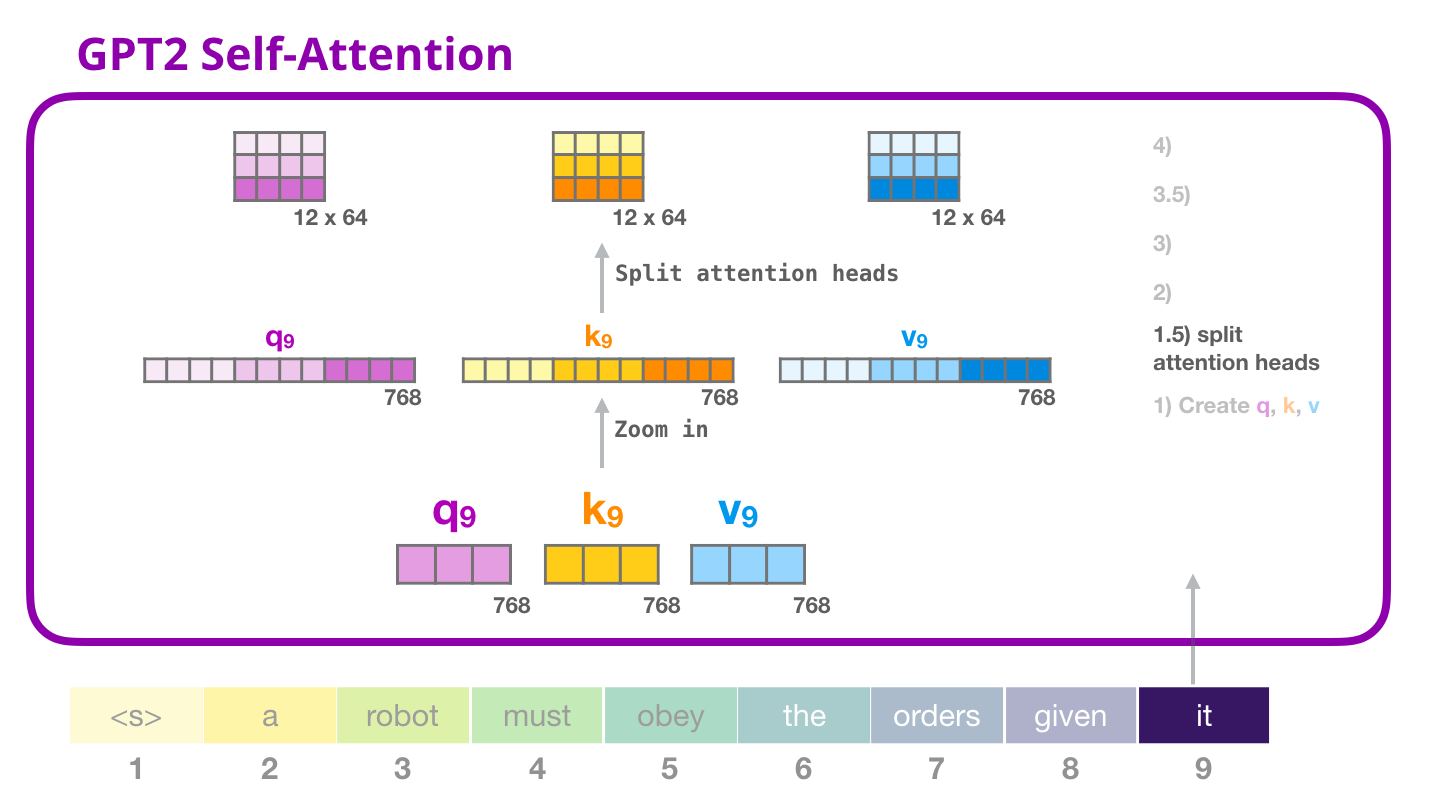
-
Mathematically,
\[\begin{array}{c} h_{i}^{\ell+1}=\text {Concat }\left(\text {head }_{1}, \ldots, \text { head}_{K}\right) O^{\ell} \\ \text { head }_{k}=\text {Attention }\left(Q^{k, \ell} h_{i}^{\ell}, K^{k, \ell} h_{j}^{\ell}, V^{k, \ell} h_{j}^{\ell}\right) \end{array}\]- where \(Q^{k, \ell}, K^{k, \ell}, V^{k, \ell}\) are the learnable weights of the \(k^{\prime}\)-th attention head and \(O^{\ell}\) is a downprojection to match the dimensions of \(h_{i}^{\ell+1}\) and \(h_{i}^{\ell}\) across layers.
-
Multiple heads allow the attention mechanism to essentially ‘hedge its bets’, looking at different transformations or aspects of the hidden features from the previous layer. More on this in the section on Why Multiple Heads of Attention? Why Attention?.
Managing computational load due to multi-head attention
- Unfortunately, multi-head attention really increases the computational load. Computing attention was already the bulk of the work, and we just multiplied it by however many heads we want to use. To get around this, we can re-use the trick of projecting everything into a lower-dimensional embedding space. This shrinks the matrices involved which dramatically reduces the computation time.
- To see how this plays out, we can continue looking at matrix shapes. Tracing the matrix shape through the branches and weaves of the multi-head attention blocks requires three more numbers.

-
The \([n \times d_{model}]\) sequence of embedded words serves as the basis for everything that follows. In each case there is a matrix, \(W_v\), \(W_q\),, and \(W_k\), (all shown unhelpfully as “Linear” blocks in the architecture diagram) that transforms the original sequence of embedded words into the values matrix, \(V\), the queries matrix, \(Q\), and the keys matrix, \(K\). \(K\) and \(Q\) have the same shape, \([n \times d_k]\), but \(V\) can be different, \([n \times d_v]\). It confuses things a little that \(d_k\) and \(d_v\) are the same in the paper, but they don’t have to be. An important aspect of this setup is that each attention head has its own \(W_v\), \(W_q\), and \(W_k\) transforms. That means that each head can zoom in and expand the parts of the embedded space that it wants to focus on, and it can be different than what each of the other heads is focusing on.
-
The result of each attention head has the same shape as \(V\). Now we have the problem of h different result vectors, each attending to different elements of the sequence. To combine these into one, we exploit the powers of linear algebra, and just concatenate all these results into one giant \([n \times h * d_v]\) matrix. Then, to make sure it ends up in the same shape it started, we use one more transform with the shape \([h * d_v \times d_{model}]\).
-
Here’s all of the that from the paper, stated tersely.
\[\begin{aligned} \operatorname{MultiHead}(Q, K, V) &=\operatorname{Concat}\left(\operatorname{head}_{1}, \ldots, \text { head }_{\mathrm{h}}\right) W^{O} \\ \text { where head } &=\operatorname{Attention}\left(Q W_{i}^{Q}, K W_{i}^{K}, V W_{i}^{V}\right) \end{aligned}\]- where the projections are parameter matrices \(W_{i}^{Q} \in \mathbb{R}^{d_{\text {model }} \times d_{k}}, W_{i}^{K} \in \mathbb{R}^{d_{\text {model }} \times d_{k}}, W_{i}^{V} \in \mathbb{R}^{d_{\text {model }} \times d_{v}}\) and \(W^{O} \in \mathbb{R}^{h d_{v} \times d_{\text {model }}}\).
Why have multiple attention heads?
- Per Eugene Yan’s Some Intuition on Attention and the Transformer blog, multiple heads lets the model consider multiple words simultaneously. Because we use the softmax function in attention, it amplifies the highest value while squashing the lower ones. As a result, each head tends to focus on a single element.
- Consider the sentence: “The chicken crossed the road carelessly”. The following words are relevant to “crossed” and should be attended to:
- The “chicken” is the subject doing the crossing.
- The “road” is the object being crossed.
- The crossing is done “carelessly”.
- If we had a single attention head, we might only focus on a single word, either “chicken”, “road”, or “crossed”. Multiple heads let us attend to several words. It also provides redundancy, where if any single head fails, we have the other attention heads to rely on.
Cross-Attention
-
The final step in getting the full transformer up and running is the connection between the encoder and decoder stacks, the cross attention block. We’ve saved it for last and, thanks to the groundwork we’ve laid, there’s not a lot left to explain.
-
Cross-attention works just like self-attention with the exception that the key matrix \(K\) and value matrix \(V\) are based on the output of the encoder stack (i.e., the final encoder layer), rather than the output of the previous decoder layer. The query matrix \(Q\) is still calculated from the results of the previous decoder layer. This is the channel by which information from the source sequence makes its way into the target sequence and steers its creation in the right direction. It’s interesting to note that the same embedded source sequence (output from the final layer in the encoder stack) is provided to every layer of the decoder, supporting the notion that successive layers provide redundancy and are all cooperating to perform the same task. The following figure with the Transformer architecture highlights the cross-attention piece within the transformer architecture.

Dropout
- Per the original Transformer paper, dropout is applied to the output of each “sub-layer” (where a “sub-layer” refers to the self/cross multi-head attention layers as well as the position-wise feedfoward networks.), before it is added to the sub-layer input and normalized. In addition, it is also applied dropout to the sums of the embeddings and the positional encodings in both the encoder and decoder stacks. For the base model, the original Transformer use a rate of \(P_{drop} = 0.1\).
- Thus, from a code perspective, the sequence of actions can be summarized as follows:
x2 = SubLayer(x)
x2 = torch.nn.dropout(x2, p=0.1)
x = nn.LayerNorm(x2 + x)
- For more details, please refer The Annotated Transformer.
Skip connections
- Skip connections, introduced in Deep Residual Learning for Image Recognition by He et al. (2015), occur around the Multi-Head Attention blocks, and around the element wise Feed Forward blocks in the blocks labeled “Add and Norm”. In skip connections, a copy of the input is added to the output of a set of calculations. The inputs to the attention block are added back in to its output. The inputs to the element-wise feed forward block are added to its outputs. The following figure shows the Transformer architecture highlighting the “Add and Norm” blocks, representing the residual connections and LayerNorm blocks.

- Skip connections serve two purposes:
- They help keep the gradient smooth, which is a big help for backpropagation. Attention is a filter, which means that when it’s working correctly it will block most of what tries to pass through it. The result of this is that small changes in a lot of the inputs may not produce much change in the outputs if they happen to fall into channels that are blocked. This produces dead spots in the gradient where it is flat, but still nowhere near the bottom of a valley. These saddle points and ridges are a big tripping point for backpropagation. Skip connections help to smooth these out. In the case of attention, even if all of the weights were zero and all the inputs were blocked, a skip connection would add a copy of the inputs to the results and ensure that small changes in any of the inputs will still have noticeable changes in the result. This keeps gradient descent from getting stuck far away from a good solution. Skip connections have become popular because of how they improve performance since the days of the ResNet image classifier. They are now a standard feature in neural network architectures. The figure below (source) shows the effect that skip connections have by comparing a ResNet with and without skip connections. The slopes of the loss function hills are are much more moderate and uniform when skip connections are used. If you feel like taking a deeper dive into how the work and why, there’s a more in-depth treatment in this post. The following diagram shows the comparison of loss surfaces with and without skip connections.

- The second purpose of skip connections is specific to transformers —- preserving the original input sequence. Even with a lot of attention heads, there’s no guarantee that a word will attend to its own position. It’s possible for the attention filter to forget entirely about the most recent word in favor of watching all of the earlier words that might be relevant. A skip connection takes the original word and manually adds it back into the signal, so that there’s no way it can be dropped or forgotten. This source of robustness may be one of the reasons for transformers’ good behavior in so many varied sequence completion tasks.
- They help keep the gradient smooth, which is a big help for backpropagation. Attention is a filter, which means that when it’s working correctly it will block most of what tries to pass through it. The result of this is that small changes in a lot of the inputs may not produce much change in the outputs if they happen to fall into channels that are blocked. This produces dead spots in the gradient where it is flat, but still nowhere near the bottom of a valley. These saddle points and ridges are a big tripping point for backpropagation. Skip connections help to smooth these out. In the case of attention, even if all of the weights were zero and all the inputs were blocked, a skip connection would add a copy of the inputs to the results and ensure that small changes in any of the inputs will still have noticeable changes in the result. This keeps gradient descent from getting stuck far away from a good solution. Skip connections have become popular because of how they improve performance since the days of the ResNet image classifier. They are now a standard feature in neural network architectures. The figure below (source) shows the effect that skip connections have by comparing a ResNet with and without skip connections. The slopes of the loss function hills are are much more moderate and uniform when skip connections are used. If you feel like taking a deeper dive into how the work and why, there’s a more in-depth treatment in this post. The following diagram shows the comparison of loss surfaces with and without skip connections.
Why have skip connections?
- Per Eugene Yan’s Some Intuition on Attention and the Transformer blog, because attention acts as a filter, it blocks most information from passing through. As a result, a small change to the inputs of the attention layer may not change the outputs, if the attention score is tiny or zero. This can lead to flat gradients or local optima.
- Skip connections help dampen the impact of poor attention filtering. Even if an input’s attention weight is zero and the input is blocked, skip connections add a copy of that input to the output. This ensures that even small changes to the input can still have noticeable impact on the output. Furthermore, skip connections preserve the input sentence: There’s no guarantee that a context word will attend to itself in a transformer. Skip connections ensure this by taking the context word vector and adding it to the output.
Layer normalization
- Normalization is a step that pairs well with skip connections. There’s no reason they necessarily have to go together, but they both do their best work when placed after a group of calculations, like attention or a feed forward neural network.
- The short version of layer normalization is that the values of the matrix are shifted to have a mean of zero and scaled to have a standard deviation of one. The following diagram shows several distributions being normalized.

- The longer version is that in systems like transformers, where there are a lot of moving pieces and some of them are something other than matrix multiplications (such as softmax operators or rectified linear units), it matters how big values are and how they’re balanced between positive and negative. If everything is linear, you can double all your inputs, and your outputs will be twice as big, and everything will work just fine. Not so with neural networks. They are inherently nonlinear, which makes them very expressive but also sensitive to signals’ magnitudes and distributions. Normalization is a technique that has proven useful in maintaining a consistent distribution of signal values each step of the way throughout many-layered neural networks. It encourages convergence of parameter values and usually results in much better performance.
- To understand the different types of normalization techniques, please refer Normalization Methods which includes batch normalization, a close cousin of the layer normalization used in transformers.
Softmax
-
The argmax function is “hard” in the sense that the highest value wins, even if it is only infinitesimally larger than the others. If we want to entertain several possibilities at once, it’s better to have a “soft” maximum function, which we get from softmax. To get the softmax of the value \(x\) in a vector, divide the exponential of \(x\), \(e^x\), by the sum of the exponentials of all the values in the vector. This converts the (unnormalized) logits/energy values into (normalized) probabilities \(\in [0, 1]\), with all summing up to 1.
-
The softmax is helpful here for three reasons. First, it converts our de-embedding results vector from an arbitrary set of values to a probability distribution. As probabilities, it becomes easier to compare the likelihood of different words being selected and even to compare the likelihood of multi-word sequences if we want to look further into the future.
-
Second, it thins the field near the top. If one word scores clearly higher than the others, softmax will exaggerate that difference (owing to the “exponential” operation), making it look almost like an argmax, with the winning value close to one and all the others close to zero. However, if there are several words that all come out close to the top, it will preserve them all as highly probable, rather than artificially crushing close second place results, which argmax is susceptible to. You might be thinking what the difference between standard normalization and softmax is – after all, both rescale the logits between 0 and 1. By using softmax, we are effectively “approximating” argmax as indicated earlier while gaining differentiability. Rescaling doesn’t weigh the max significantly higher than other logits, whereas softmax does due to its “exponential” operation. Simply put, softmax is a “softer” argmax.
-
Third, softmax is differentiable, meaning we can calculate how much each element of the results will change, given a small change in any of the input elements. This allows us to use it with backpropagation to train our transformer.
-
Together the de-embedding transform (shown as the Linear block below) and a softmax function complete the de-embedding process. The following diagram shows the de-embedding steps in the architecture diagram (source: Transformers paper).

Stacking Transformer Layers
- While we were laying the foundations above, we showed that an attention block and a feed forward block with carefully chosen weights were enough to make a decent language model. Most of the weights were zeros in our examples, a few of them were ones, and they were all hand picked. When training from raw data, we won’t have this luxury. At the beginning the weights are all chosen randomly, most of them are close to zero, and the few that aren’t probably aren’t the ones we need. It’s a long way from where it needs to be for our model to perform well.
- Stochastic gradient descent through backpropagation can do some pretty amazing things, but it relies a lot on trial-and-error. If there is just one way to get to the right answer, just one combination of weights necessary for the network to work well, then it’s unlikely that it will find its way. But if there are lots of paths to a good solution, chances are much better that the model will get there.
- Having a single attention layer (just one multi-head attention block and one feed forward block) only allows for one path to a good set of transformer parameters. Every element of every matrix needs to find its way to the right value to make things work well. It is fragile and brittle, likely to get stuck in a far-from-ideal solution unless the initial guesses for the parameters are very very lucky.
- The way transformers sidestep this problem is by having multiple attention layers, each using the output of the previous one as its input. The use of skip connections make the overall pipeline robust to individual attention blocks failing or giving wonky results. Having multiples means that there are others waiting to take up the slack. If one should go off the rails, or in any way fail to live up to its potential, there will be another downstream that has another chance to close the gap or fix the error. The paper showed that more layers resulted in better performance, although the improvement became marginal after 6.
- Another way to think about multiple layers is as a conveyor belt assembly line. Each attention block and feedforward block has the chance to pull inputs off the line, calculate useful attention matrices and make next word predictions. Whatever results they produce, useful or not, get added back onto the conveyer, and passed to the next layer. The following diagram shows the transformer redrawn as a conveyor belt:

- This is in contrast to the traditional description of many-layered neural networks as “deep”. Thanks to skip connections, successive layers don’t provide increasingly sophisticated abstraction as much as they provide redundancy. Whatever opportunities for focusing attention and creating useful features and making accurate predictions were missed in one layer can always be caught by the next. Layers become workers on the assembly line, where each does what it can, but doesn’t worry about catching every piece, because the next worker will catch the ones they miss.
Why have multiple attention layers?
- Per Eugene Yan’s Some Intuition on Attention and the Transformer blog, multiple attention layers builds in redundancy (on top of having multiple attention heads). If we only had a single attention layer, that attention layer would have to do a flawless job—this design could be brittle and lead to suboptimal outcomes. We can address this via multiple attention layers, where each one uses the output of the previous layer with the safety net of skip connections. Thus, if any single attention layer messed up, the skip connections and downstream layers can mitigate the issue.
- Stacking attention layers also broadens the model’s receptive field. The first attention layer produces context vectors by attending to interactions between pairs of words in the input sentence. Then, the second layer produces context vectors based on pairs of pairs, and so on. With more attention layers, the Transformer gains a wider perspective and can attend to multiple interaction levels within the input sentence.
Transformer Encoder and Decoder
- The Transformer model has two parts: encoder and decoder. Both encoder and decoder are mostly identical (with a few differences) and are comprised of a stack of transformer blocks. Each block is comprised of a combination of multi-head attention blocks, positional feedforward layers, residual connections and layer normalization blocks.
- The attention layers from the encoder and decoder have the following differences:
- The encoder only has self-attention blocks while the decoder has a cross-attention encoder-decoder layer sandwiched between the self-attention layer and the feedforward neural network.
- Also, the self-attention blocks are masked to ensure causal predictions (i.e., the prediction of token \(N\) only depends on the previous \(N - 1\) tokens, and not on the future ones).
- Each of the encoding/decoding blocks contains many stacked encoders/decoder transformer blocks. The Transformer encoder is a stack of six encoders, while the decoder is a stack of six decoders. The initial layers capture more basic patterns (broadly speaking, basic syntactic patterns), whereas the last layers can detect more sophisticated ones, similar to how convolutional networks learn to look for low-level features such as edges and blobs of color in the initial layers while the mid layers focus on learning high-level features such as object shapes and textures the later layers focus on detecting the entire objects themselves (using textures, shapes and patterns learnt from earlier layers as building blocks).
- The six encoders and decoders are identical in structure but do not share weights. Check weights shared by different parts of a transformer model for a detailed discourse on weight sharing opportunities within the Transformer layers.
- For more on the pros and cons of the encoder and decoder stack, refer Autoregressive vs. Autoencoder Models.
Decoder stack
The decoder, which follows the auto-regressive property, i.e., consumes the tokens generated so far to generate the next one, is used standalone for generation tasks, such as tasks in the domain of natural language generation (NLG), for e.g., such as summarization, translation, or abstractive question answering. Decoder models are typically trained with an objective of predicting the next token, i.e., “autoregressive blank infilling”.
- As we laid out in the section on Sampling a Sequence of Output Words, the decoder can complete partial sequences and extend them as far as you want. OpenAI created the generative pre-training (GPT) family of models to do just this, by training on a predicting-the-next-token objective. The architecture they describe in this report should look familiar. It is a transformer with the encoder stack and all its connections surgically removed. What remains is a 12 layer decoder stack. The following diagram from the GPT-1 paper Improving Language Understanding by Generative Pre-Training shows the architecture of the GPT family of models:

- Any time you come across a generative/auto-regressive model, such as GPT-X, LLaMA, Copilot, etc., you’re probably seeing the decoder half of a transformer in action.
Encoder stack
The encoder, is typically used standalone for content understanding tasks, such as tasks in the domain of natural language understanding (NLU) that involve classification, for e.g., sentiment analysis, or extractive question answering. Encoder models are typically trained with a “fill in the blanks”/”blank infilling” objective – reconstructing the original data from masked/corrupted input (i.e., by randomly sampling tokens from the input and replacing them with
[MASK]elements, or shuffling sentences in random order if it’s the next sentence prediction task). In that sense, an encoder can be thought of as an auto-encoder which seeks to denoise a partially corrupted input, i.e., “Denoising Autoencoder” (DAE) and aim to recover the original undistorted input.
- Almost everything we’ve learned about the decoder applies to the encoder too. The biggest difference is that there’s no explicit predictions being made at the end that we can use to judge the rightness or wrongness of its performance. Instead, the end product of an encoder stack is an abstract representation in the form of a sequence of vectors in an embedded space. It has been described as a pure semantic representation of the sequence, divorced from any particular language or vocabulary, but this feels overly romantic to me. What we know for sure is that it is a useful signal for communicating intent and meaning to the decoder stack.
-
Having an encoder stack opens up the full potential of transformers instead of just generating sequences, they can now translate (or transform) the sequence from one language to another. Training on a translation task is different than training on a sequence completion task. The training data requires both a sequence in the language of origin, and a matching sequence in the target language. The full language of origin is run through the encoder (no masking this time, since we assume that we get to see the whole sentence before creating a translation) and the result, the output of the final encoder layer is provided as an input to each of the decoder layers. Then sequence generation in the decoder proceeds as before, but this time with no prompt to kick it off.
-
Any time you come across an encoder model that generates semantic embeddings, such as BERT, ELMo, etc., you’re likely seeing the encoder half of a transformer in action.
Putting it all together: The Transformer Architecture
- The Transformer architecture combines the individual encoder/decoder models. The encoder takes the input and encodes it into fixed-length query, key, and vector tensors (analogous to the fixed-length context vector in the original paper by Bahdanau et al. (2015)) that introduced attention. These tensors are passed onto the decoder which decodes it into the output sequence.
-
The encoder (left) and decoder (right) of the transformer is shown below:

-
Note that the multi-head attention in the encoder is the scaled dot-product multi-head self attention, while that in the initial layer in the decoder is the masked scaled dot-product multi-head self attention and the middle layer (which enables the decoder to attend to the encoder) is the scaled dot-product multi-head cross attention.
-
Re-drawn vectorized versions from DAIR.AI are as follows:


-
- The full model architecture of the transformer – from fig. 1 and 2 in Vaswani et al. (2017) – is as follows:

- Here is an illustrated version of the overall Transformer architecture from Abdullah Al Imran:

- As a walk-through exercise, the following diagram (source: CS330 slides) shows an sample input sentence “Joe Biden is the US President” being fed in as input to the Transformer. The various transformations that occur as the input vector is processed are:
- Input sequence: \(I\) = “Joe Biden is the US President”.
- Tokenization: \(I \in {\mid \text { vocab } \mid}^{T}\).
- Input embeddings lookup: \(E \in \mathbb{R}^{T \times d}\).
- Inputs to Transformer block: \(X \in \mathbb{R}^{T \times d}\).
- Obtaining three separate linear projections of input \(X\) (queries, keys, and values): \(X_Q=X W_Q, \quad X_K=X W_K, \quad X_V=X W_V\).
- Calculating self-attention: \(A=\operatorname{sm}\left(X_Q X_K^{\top}\right) X_V\) (the scaling part is missing in the figure below – you can reference the section on Types of Attention: Additive, Multiplicative (Dot-product), and Scaled for more).
- This is followed by a residual connection and LayerNorm.
- Feed-forward (MLP) layers which perform two linear transformations/projections of the input with a ReLU activation in between: \(\operatorname{FFN}(x)=\max \left(0, x W_1+b_1\right) W_2+b_2\)
- This is followed by a residual connection and LayerNorm.
- Output of the Transformer block: \(O \in \mathbb{R}^{T \times d}\).
- Project to vocabulary size at time \(t\): \(p_\theta^t(\cdot) \in \mathbb{R}^{\mid \text {vocab } \mid}\).

Loss function
- The encoder and decoder are jointly trained (“end-to-end”) to minimize the cross-entropy loss between the predicted probability matrix of shape
output sequence length\(\times\)vocab(right before taking the argmax on the output of the softmax to ascertain the next token to output), and theoutput sequence length-sized output vector of token IDs as the true label. - Effectively, the cross-entropy loss “pulls” the predicted probability of the correct class towards 1 during training. This is accomplished by calculating gradients of the loss function w.r.t. the model’s weights; with the model’s sigmoid/softmax output (in case of binary/multiclass classification) serving as the prediction (i.e., the pre-argmax output is utilized since argmax is not differentiable).
Implementation details
Tokenizing
-
We made it all the way through the transformer! We covered it in enough detail that there should be no mysterious black boxes left. There are a few implementation details that we didn’t dig into. You would need to know about them in order to build a working version for yourself. These last few tidbits aren’t so much about how transformers work as they are about getting neural networks to behave well. The Annotated Transformer will help you fill in these gaps.
-
In the section on One-hot encoding, we discussed that a vocabulary could be represented by a high dimensional one-hot vector, with one element associated with each word. In order to do this, we need to know exactly how many words we are going to be representing and what they are.
-
A naïve approach is to make a list of all possible words, like we might find in Webster’s Dictionary. For the English language this will give us several tens of thousands, the exact number depending on what we choose to include or exclude. But this is an oversimplification. Most words have several forms, including plurals, possessives, and conjugations. Words can have alternative spellings. And unless your data has been very carefully cleaned, it will contain typographical errors of all sorts. This doesn’t even touch on the possibilities opened up by freeform text, neologisms, slang, jargon, and the vast universe of Unicode. An exhaustive list of all possible words would be infeasibly long.
-
A reasonable fallback position would be to have individual characters serve as the building blocks, rather than words. An exhaustive list of characters is well within the capacity we have to compute. However there are a couple of problems with this. After we transform data into an embedding space, we assume the distance in that space has a semantic interpretation, that is, we assume that points that fall close together have similar meanings, and points that are far away mean something very different. That allows us to implicitly extend what we learn about one word to its immediate neighbors, an assumption we rely on for computational efficiency and from which the transformer draws some ability to generalize.
-
At the individual character level, there is very little semantic content. There are a few one character words in the English language for example, but not many. Emoji are the exception to this, but they are not the primary content of most of the data sets we are looking at. That leaves us in the unfortunate position of having an unhelpful embedding space.
-
It might still be possible to work around this theoretically, if we could look at rich enough combinations of characters to build up semantically useful sequences like words, words stems, or word pairs. Unfortunately, the features that transformers create internally behave more like a collection of input pairs than an ordered set of inputs. That means that the representation of a word would be a collection of character pairs, without their order strongly represented. The transformer would be forced to continually work with anagrams, making its job much harder. And in fact experiments with character level representations have shown the transformers don’t perform very well with them.
Per OpenAI’s Tokenizer Platform page, a helpful rule of thumb is that one token generally corresponds to ~4 characters of text for common English text. This translates to roughly \(\frac{3}{4}\) of a word (so 100 tokens ~= 75 words).
Byte pair encoding (BPE)
- Fortunately, there is an elegant solution to this called byte pair encoding, which is a simple form of data compression in which the most common pair of consecutive bytes of data is replaced with a byte that does not occur within that data. A table of the replacements is required to rebuild the original data.
- Starting with the character level representation, each character is assigned a code, its own unique byte. Then after scanning some representative data, the most common pair of bytes is grouped together and assigned a new byte, a new code. This new code is substituted back into the data, and the process is repeated.
Example
- As an example (credit: Wikipedia: Byte pair encoding), suppose the data to be encoded is:
aaabdaaabac
- The byte pair “aa” occurs most often, so it will be replaced by a byte that is not used in the data, “Z”. Now there is the following data and replacement table:
ZabdZabac
Z=aa
- Then the process is repeated with byte pair “ab”, replacing it with Y:
ZYdZYac
Y=ab
Z=aa
- The only literal byte pair left occurs only once, and the encoding might stop here. Or the process could continue with recursive byte pair encoding, replacing “ZY” with “X”:
XdXac
X=ZY
Y=ab
Z=aa
- This data cannot be compressed further by byte pair encoding because there are no pairs of bytes that occur more than once.
- To decompress the data, simply perform the replacements in the reverse order.
Applying BPE to learn new, rare, and misspelled words
-
Codes representing pairs of characters can be combined with codes representing other characters or pairs of characters to get new codes representing longer sequences of characters. There’s no limit to the length of character sequence a code can represent. They will grow as long as they need to in order to represent commonly repeated sequences. The cool part of byte pair encoding is that in infers which long sequences of characters to learn from the data, as opposed to dumbly representing all possible sequences. it learns to represent long words like transformer with a single byte code, but would not waste a code on an arbitrary string of similar length, such as
ksowjmckder. And because it retains all the byte codes for its single character building blocks, it can still represent weird misspellings, new words, and even foreign languages. -
When you use byte pair encoding, you get to assign it a vocabulary size, ad it will keep building new codes until reaches that size. The vocabulary size needs to be big enough, that the character strings get long enough to capture the semantic content of the the text. They have to mean something. Then they will be sufficiently rich to power transformers.
-
After a byte pair encoder is trained or borrowed, we can use it to pre-process out data before feeding it into the transformer. This breaks it the unbroken stream of text into a sequence of distinct chunks, (most of which are hopefully recognizable words) and provides a concise code for each one. This is the process called tokenization.
Teacher Forcing
- Teacher forcing is a common training technique for sequence-to-sequence models where, during training, the model is fed with the ground truth (true) target sequence at each time step as input, rather than the model’s own predictions. This helps the model learn faster and more accurately during training because it has access to the correct information at each step.
- Pros: Teacher forcing is essential because it accelerates training convergence and stabilizes learning. By using correct previous tokens as input during training, it ensures the model learns to predict the next token accurately. If we do not use teacher forcing, the hidden states of the model will be updated by a sequence of wrong predictions, errors will accumulate, making it difficult for the model to learn. This method effectively guides the model in learning the structure and nuances of language (especially during early stages of training when the predictions of the model lack coherence), leading to more coherent and contextually accurate text generation.
- Cons: With teacher forcing, when the model is deployed for inference (generating sequences), it typically does not have access to ground truth information and must rely on its own predictions, which can be less accurate. Put simply, during inference, since there is usually no ground truth available, the model will need to feed its own previous prediction back to itself for the next prediction. This discrepancy between training and inference can potentially lead to poor model performance and instability. This is known as “exposure bias” in literature, which can be mitigated using scheduled sampling.
- For more, check out What is Teacher Forcing for Recurrent Neural Networks? and What is Teacher Forcing?.
Scheduled Sampling
- Scheduled sampling is a technique used in sequence-to-sequence models, particularly in the context of training recurrent neural networks (RNNs) and sequence-to-sequence models like LSTMs and Transformers. Its primary goal is to address the discrepancy between the training and inference phases that arises due to teacher forcing, and it helps mitigate the exposure bias generated by teacher forcing.
- Scheduled sampling is thus introduced to bridge this “train-test discrepancy” gap between training and inference by gradually transitioning from teacher forcing to using the model’s own predictions during training. Here’s how it works:
- Teacher Forcing Phase:
- In the early stages of training, scheduled sampling follows a schedule where teacher forcing is dominant. This means that the model is mostly exposed to the ground truth target sequence during training.
- At each time step, the model has a high probability of receiving the true target as input, which encourages it to learn from the correct data.
- Transition Phase:
- As training progresses, scheduled sampling gradually reduces the probability of using the true target as input and increases the probability of using the model’s own predictions.
- This transition phase helps the model get accustomed to generating its own sequences and reduces its dependence on the ground truth data.
- Inference Phase:
- During inference (when the model generates sequences without access to the ground truth), scheduled sampling is typically turned off. The model relies entirely on its own predictions to generate sequences.
- Teacher Forcing Phase:
- By implementing scheduled sampling, the model learns to be more robust and capable of generating sequences that are not strictly dependent on teacher-forced inputs. This mitigates the exposure bias problem, as the model becomes more capable of handling real-world scenarios where it must generate sequences autonomously.
- In summary, scheduled sampling is a training strategy for sequence-to-sequence models that gradually transitions from teacher forcing to using the model’s own predictions, helping to bridge the gap between training and inference and mitigating the bias generated by teacher forcing. This technique encourages the model to learn more robust and accurate sequence generation.
Decoder Outputs: Shifted Right
- In the architectural diagram of the Transformer shown below, the output embedding that is “shifted right”. This shifting is done during training, where the decoder is given the correct output at that step (e.g., the translation of a sentence in the original Transformer decoder) as input but shifted one position to the right. This means that the token at each position in the input is the token that should have been predicted at the previous step.
- This shift-right ensures that the prediction for a particular position (say position \(i\)) is only dependent on the known outputs at positions less than \(i\). Essentially, it prevents the model from “cheating” by seeing the correct output for position \(i\) when predicting position \(i\).

Label Smoothing as a Regularizer
- During training, they employ label smoothing which penalizes the model if it gets overconfident about a particular choice. This hurts perplexity, as the model learns to be more unsure, but improves accuracy and BLEU score.
- They implement label smoothing using the KL div loss. Instead of using a one-hot target distribution, we create a distribution that has a reasonably high confidence of the correct word and the rest of the smoothing mass distributed throughout the vocabulary.
Scaling Issues
- A key issue motivating the final Transformer architecture is that the features for words after the attention mechanism might be at different scales or magnitudes. This can be due to some words having very sharp or very distributed attention weights \(w_{i j}\) when summing over the features of the other words. Scaling the dot-product attention by the square-root of the feature dimension helps counteract this issue.
- Additionally, at the individual feature/vector entries level, concatenating across multiple attention heads-each of which might output values at different scales-can lead to the entries of the final vector \(h_{i}^{\ell+1}\) having a wide range of values. Following conventional ML wisdom, it seems reasonable to add a normalization layer into the pipeline. As such, Transformers overcome this issue with LayerNorm, which normalizes and learns an affine transformation at the feature level.
- Finally, the authors propose another ‘trick’ to control the scale issue: a position-wise 2-layer MLP with a special structure. After the multi-head attention, they project \(h_{i}^{\ell+1}\) to a (absurdly) higher dimension by a learnable weight, where it undergoes the ReLU non-linearity, and is then projected back to its original dimension followed by another normalization:
- Since LayerNorm and scaled dot-products (supposedly) didn’t completely solve the highlighted scaling issues, the over-parameterized feed-forward sub-layer was utilized. In other words, the big MLP is a sort of hack to re-scale the feature vectors independently of each other. According to Jannes Muenchmeyer, the feed-forward sub-layer ensures that the Transformer is a universal approximator. Thus, projecting to a very high dimensional space, applying a non-linearity, and re-projecting to the original dimension allows the model to represent more functions than maintaining the same dimension across the hidden layer would. The final picture of a Transformer layer looks like this:

- The Transformer architecture is also extremely amenable to very deep networks, enabling the NLP community to scale up in terms of both model parameters and, by extension, data. Residual connections between the inputs and outputs of each multi-head attention sub-layer and the feed-forward sub-layer are key for stacking Transformer layers (but omitted from the diagram for clarity).
The relation between transformers and Graph Neural Networks
GNNs build representations of graphs
-
Let’s take a step away from NLP for a moment.
-
Graph Neural Networks (GNNs) or Graph Convolutional Networks (GCNs) build representations of nodes and edges in graph data. They do so through neighbourhood aggregation (or message passing), where each node gathers features from its neighbours to update its representation of the local graph structure around it. Stacking several GNN layers enables the model to propagate each node’s features over the entire graph—from its neighbours to the neighbours’ neighbours, and so on.
-
Take the example of this emoji social network below (source): The node features produced by the GNN can be used for predictive tasks such as identifying the most influential members or proposing potential connections.

-
In their most basic form, GNNs update the hidden features \(h\) of node \(i\) (for example, 😆) at layer \(\ell\) via a non-linear transformation of the node’s own features \(h_{i}^{\ell}\) added to the aggregation of features \(h_{j}^{\ell}\) from each neighbouring node \(j \in \mathcal{N}(i)\):
\[h_{i}^{\ell+1}=\sigma\left(U^{\ell} h_{i}^{\ell}+\sum_{j \in \mathcal{N}(i)}\left(V^{\ell} h_{j}^{\ell}\right)\right)\]- where \(U^{\ell}, V^{\ell}\) are learnable weight matrices of the GNN layer and \(\sigma\) is a non-linear function such as ReLU. In the example, (😆) {😘, 😎, 😜, 🤩}.
-
The summation over the neighbourhood nodes \(j \in \mathcal{N}(i)\) can be replaced by other input sizeinvariant aggregation functions such as simple mean/max or something more powerful, such as a weighted sum via an attention mechanism.
-
Does that sound familiar? Maybe a pipeline will help make the connection (figure source):

- If we were to do multiple parallel heads of neighbourhood aggregation and replace summation over the neighbours \(j\) with the attention mechanism, i.e., a weighted sum, we’d get the Graph Attention Network (GAT). Add normalization and the feed-forward MLP, and voila, we have a Graph Transformer! Transformers are thus a special case of GNNs – they are just GNNs with multi-head attention.
Sentences are fully-connected word graphs
- To make the connection more explicit, consider a sentence as a fully-connected graph, where each word is connected to every other word. Now, we can use a GNN to build features for each node (word) in the graph (sentence), which we can then perform NLP tasks with as shown in the figure (source) below.

-
Broadly, this is what Transformers are doing: they are GNNs with multi-head attention as the neighbourhood aggregation function. Whereas standard GNNs aggregate features from their local neighbourhood nodes \(j \in \mathcal{N}(i)\), Transformers for NLP treat the entire sentence \(\mathcal{S}\) as the local neighbourhood, aggregating features from each word \(j \in \mathcal{S}\) at each layer.
-
Importantly, various problem-specific tricks—such as position encodings, causal/masked aggregation, learning rate schedules and extensive pre-training—are essential for the success of Transformers but seldom seem in the GNN community. At the same time, looking at Transformers from a GNN perspective could inspire us to get rid of a lot of the bells and whistles in the architecture.
Inductive biases of transformers
- Based on the above discussion, we’ve established that transformers are indeed a special case of Graph Neural Networks (GNNs) owing to their architecture level commonalities. Relational inductive biases, deep learning, and graph networks by Battaglia et al. (2018) from DeepMind/Google, MIT and the University of Edinburgh offers a great overview of the relational inductive biases of various neural net architectures, summarized in the table below from the paper. Each neural net architecture exhibits varying degrees of relational inductive biases. Transformers fall somewhere between RNNs and GNNs in the table below (source).

- YouTube Video from UofT CSC2547: Relational inductive biases, deep learning, and graph networks; Slides by KAIST on inductive biases, graph neural networks, attention and relational inference
Time complexity: RNNs vs. Transformers
- RNNs and Transformers have different time complexities, which significantly impact their runtime performance, especially on long sequences. This section offers a detailed explanation of the time complexities of RNNs and Transformers, including the reasoning behind each term in the complexities.
RNNs
- Time Complexity: \(O(n \cdot d^2)\)
- Explanation:
- \(n\): This represents the length of the input sequence. RNNs process sequences one step at a time, so they need to iterate through all \(n\) time steps.
- \(d\): This represents the dimensionality of the hidden state.
- \(d^2\): This term arises because at each time step, an RNN performs operations that involve the hidden state. Specifically, each step involves matrix multiplications that have a computational cost of \(O(d^2)\). The key operations are:
- Hidden State Update: For a simple RNN, the hidden state update is computed as \(h_t = \tanh(W_h h_{t-1} + W_x x_t)\). Here, \(W_h\) and \(W_x\) are weight matrices of size \(d \times d\) and \(d \times \text{input\_dim}\), respectively.
- The matrix multiplication \(W_h h_{t-1}\) dominates the computation and contributes \(O(d^2)\) to the complexity because multiplying a \(d \times d\) matrix with a \(d\)-dimensional vector requires \(d^2\) operations.
- Therefore, for each of the \(n\) time steps, the \(d^2\) operations need to be performed, leading to the overall time complexity of \(O(n \cdot d^2)\).
- Explanation:
Transformers
- Time Complexity: \(O(n^2 \cdot d)\)
- Explanation:
- \(n\): This represents the length of the input sequence.
- \(n^2\): This term arises from the self-attention mechanism used in Transformers. In self-attention, each token in the sequence attends to every other token, requiring the computation of attention scores for all pairs of tokens. This results in \(O(n^2)\) pairwise comparisons.
- \(d\): This represents the dimensionality of the model. The attention mechanism involves projecting the input into query, key, and value vectors of size \(d\), and computing dot products between queries and keys, which are then scaled and used to weight the values. The operations involved are:
- Projection: Each input token is projected into three different \(d\)-dimensional spaces (query, key, value), resulting in a complexity of \(O(nd)\) for this step.
- Dot Products: Computing the dot product between each pair of query and key vectors results in \(O(n^2 d)\) operations.
- Weighting and Summing: Applying the attention weights to the value vectors and summing them up also involves \(O(n^2 d)\) operations.
- Therefore, the overall time complexity for the self-attention mechanism in Transformers is \(O(n^2 \cdot d)\).
- Explanation:
Comparative Analysis
- RNNs: The linear time complexity with respect to the sequence length makes RNNs potentially faster for shorter sequences. However, their sequential nature can make parallelization challenging, leading to slower processing times for long sequences on modern hardware optimized for parallel computations. Put simply, the dependency on previous time steps means that RNNs cannot fully leverage parallel processing, which is a significant drawback on modern hardware optimized for parallel computations.
- Transformers: The quadratic time complexity with respect to the sequence length means that Transformers can be slower for very long sequences. However, their highly parallelizable architecture often results in faster training and inference times on modern GPUs, especially for tasks involving long sequences or large datasets. This parallelism makes them more efficient in practice, especially for tasks involving long sequences or large datasets. The ability to handle dependencies across long sequences without being constrained by the sequential nature of RNNs gives Transformers a significant advantage in many applications.
Practical Implications
- For tasks involving short to moderately long sequences, RNNs can be efficient and effective.
- For tasks involving long sequences, Transformers are generally preferred due to their parallel processing capabilities, despite their higher theoretical time complexity.
Summary
- RNNs: \(O(n \cdot d^2)\) – Efficient for shorter sequences, but limited by sequential processing.
- Transformers: \(O(n^2 \cdot d)\) – Better suited for long sequences due to parallel processing capabilities, despite higher theoretical complexity.
Lessons Learned
Transformers: merging the worlds of linguistic theory and statistical NLP using fully connected graphs
-
Now that we’ve established a connection between Transformers and GNNs, let’s throw some ideas around. For one, are fully-connected graphs the best input format for NLP?
-
Before statistical NLP and ML, linguists like Noam Chomsky focused on developing formal theories of linguistic structure, such as syntax trees/graphs. Tree LSTMs already tried this, but maybe Transformers/GNNs are better architectures for bringing together the two worlds of linguistic theory and statistical NLP? For example, a very recent work from MILA and Stanford explores augmenting pre-trained Transformers such as BERT with syntax trees [Sachan et al., 2020. The figure below from Wikipedia: Syntactic Structures shows a tree diagram of the sentence “Colorless green ideas sleep furiously”:

Long term dependencies
-
Another issue with fully-connected graphs is that they make learning very long-term dependencies between words difficult. This is simply due to how the number of edges in the graph scales quadratically with the number of nodes, i.e., in an \(n\) word sentence, a Transformer/GNN would be doing computations over \(n^{2}\) pairs of words. Things get out of hand for very large \(n\).
-
The NLP community’s perspective on the long sequences and dependencies problem is interesting: making the attention mechanism sparse or adaptive in terms of input size, adding recurrence or compression into each layer, and using Locality Sensitive Hashing for efficient attention are all promising new ideas for better transformers. See Maddison May’s excellent survey on long-term context in Transformers for more details.
-
It would be interesting to see ideas from the GNN community thrown into the mix, e.g., Binary Partitioning for sentence graph sparsification seems like another exciting approach. BP-Transformers recursively sub-divide sentences into two until they can construct a hierarchical binary tree from the sentence tokens. This structural inductive bias helps the model process longer text sequences in a memory-efficient manner. The following figure from Ye et al. (2019) shows binary partitioning for sentence graph sparsification.

Are Transformers learning neural syntax?
- There have been several interesting papers from the NLP community on what Transformers might be learning. The basic premise is that performing attention on all word pairs in a sentence – with the purpose of identifying which pairs are the most interesting – enables Transformers to learn something like a task-specific syntax.
- Different heads in the multi-head attention might also be ‘looking’ at different syntactic properties, as shown in the figure (source) below.

Why multiple heads of attention? Why attention?
- The optimization view of multiple attention heads is that they improve learning and help overcome bad random initializations. For instance, Analyzing Multi-Head Self-Attention: Specialized Heads Do the Heavy Lifting, the Rest Can Be Pruned and it’s accompanying post by Viota (2019) and Are Sixteen Heads Really Better than One? by Michel et al. showed that Transformer heads can be ‘pruned’ or removed after training without significant performance impact.
Benefits of Transformers compared to RNNs/GRUs/LSTMs
- The Transformer can learn longer-range dependencies than RNNs and its variants such as GRUs and LSTMs.
- The biggest benefit, however, comes from how the Transformer lends itself to parallelization. Unlike an RNN which processes a word at each time step, a key property of the Transformer is that the word at each position flows through its own path in the encoder. There are dependencies between these paths in the self-attention layer (since the self-attention layer computes how important each other word in the input sequence is to this word). However, once the self-attention output is generated, the feed-forward layer does not have those dependencies, and thus the various paths can be executed in parallel while flowing through the feed-forward layer. This is an especially useful trait in case of the Transformer encoder which can process each input word in parallel with other words after the self-attention layer. This feature, is however, not of great importance for the decoder since it generates one word at a time and thus does not utilize parallel word paths.
What would we like to fix about the transformer? / Drawbacks of Transformers
- The biggest drawback of the Transformer architecture is the quadratic computational complexity with respect to both the number of tokens (\(n\)) and the embedding size (\(d\)). This means that as sequences get longer, the time and computational resources needed for training increase significantly. A detailed discourse on this and a couple of secondary drawbacks are as below.
- Quadratic time and space complexity of the attention layer:
- Transformers use what’s known as self-attention, where each token in a sequence attends to all other tokens (including itself). This implies that the runtime of the Transformer architecture is quadratic in the length of the input sequence, which means it can be slow when processing long documents or taking characters as inputs. If you have a sequence of $$n $$ tokens, you’ll essentially have to compute attention scores for each pair of tokens, resulting in $$n^2 $$ (quadratic) computations. In other words, computing all pairs of interactions (i.e., attention over all word-pairs) during self-attention means our computation grows quadratically with the sequence length, i.e., \(O(T^2 d)\), where \(T\) is the sequence length, and \(d\) is the dimensionality.
- In a graph context, self-attention mandates that the number of edges in the graph to scale quadratically with the number of nodes, i.e., in an \(n\) word sentence, a Transformer would be doing computations over \(n^{2}\) pairs of words. Note that for recurrent models, it only grew linearly.
- This implies a large parameter count (implying high memory footprint) and thus, high computational complexity.
- Say, \(d = 1000\). So, for a single (shortish) sentence, \(T \leq 30 \Rightarrow T^{2} \leq 900 \Rightarrow T^2 d \approx 900K\). Note that in practice, we set a bound such as \(T = 512\). Imagine working on long documents with \(T \geq 10,000\)?!
- High compute requirements has a negative impact on power and battery life requirements, especially for portable device targets.
- Similarly, for storing these attention scores, you’d need space that scales with $$n^2 $$, leading to a quadratic space complexity.
- This becomes problematic for very long sequences as both the computation time and memory usage grow quickly, limiting the practical use of standard transformers for lengthy inputs.
- Overall, a transformer requires higher computational power (and thus, lower battery life) and memory footprint compared to its conventional counterparts.
- Wouldn’t it be nice for Transformers if we didn’t have to compute pair-wise interactions between each word pair in the sentence? Recent studies such as the following show that decent performance levels can be achieved without computing interactions between all word-pairs (such as by approximating pair-wise attention).
- Quadratic time complexity of linear layers w.r.t. embedding size $$d $$:
- In Transformers, after calculating the attention scores, the result is passed through linear layers, which have weights that scale with the dimension of the embeddings. If your token is represented by an embedding of size $$d $$, and if $$d $$ is greater than $$n $$ (the number of tokens), then the computation associated with these linear layers can also be demanding.
- The complexity arises because for each token, you’re doing operations in a $$d $$-dimensional space. For densely connected layers, if $$d $$ grows, the number of parameters and hence computations grows quadratically.
- Positional Sinusoidal Embedding:
- Transformers, in their original design, do not inherently understand the order of tokens (i.e., they don’t recognize sequences). To address this, positional information is added to the token embeddings.
- The original Transformer model (by Vaswani et al.) proposed using sinusoidal functions to generate these positional embeddings. This method allows models to theoretically handle sequences of any length (since sinusoids are periodic and continuous), but it might not be the most efficient or effective way to capture positional information, especially for very long sequences or specialized tasks. Hence, it’s often considered a limitation or area of improvement, leading to newer positional encoding methods like Rotary Positional Embeddings (RoPE).
- Data appetite of Transformers vs. sample-efficient architectures:
- Furthermore, compared to CNNs, the sample complexity (i.e., data appetite) of transformers is obscenely high. CNNs are still sample efficient, which makes them great candidates for low-resource tasks. This is especially true for image/video generation tasks where an exceptionally large amount of data is needed, even for CNN architectures (and thus implies that Transformer architectures would have a ridiculously high data requirement). For example, the recent CLIP architecture by Radford et al. was trained with CNN-based ResNets as vision backbones (and not a ViT-like transformer architecture).
- Put simply, while Transformers do offer accuracy lifts once their data requirement is satisfied, CNNs offer a way to deliver reasonable performance in tasks where the amount of data available is not exceptionally high. Both architectures thus have their use-cases.
Why is training Transformers so hard?
- Reading new Transformer papers makes me feel that training these models requires something akin to black magic when determining the best learning rate schedule, warmup strategy and decay settings. This could simply be because the models are so huge and the NLP tasks studied are so challenging.
- But recent results suggest that it could also be due to the specific permutation of normalization and residual connections within the architecture.
Transformers: Extrapolation engines in high-dimensional space
- The fluency of Transformers can be tracked back to extrapolation in a high dimensional space. That is what they do: capturing of high abstractions of semantic structures while learning, matching and merging those patterns on output. So any inference must be converted into a retrieval task (which then is called many names like Prompt Engineering, Chain/Tree/Graph/* of Thought, RAG, etc.), while any Transformer model is by design a giant stochastic approximation of whatever its training data it was fed.
The road ahead for Transformers
- In the field of NLP, Transformers have already established themselves as the numero uno architectural choice or the de facto standard for a plethora of NLP tasks.
- Likewise, in the field of vision, an updated version of ViT was second only to a newer approach that combines CNNs with transformers on the ImageNet image classification task at the start of 2022. CNNs without transformers, the longtime champs, barely reached the top 10!
- It is quite likely that transformers or hybrid derivatives thereof (combining concepts of self-attention with say convolutions) will be the leading architectures of choice in the near future, especially if functional metrics (such as accuracy) are the sole optimization metrics. However, along other axes such as data, computational complexity, power/battery life, and memory footprint, transformers are currently not the best choice – which the above section on What Would We Like to Fix about the Transformer? / Drawbacks of Transformers expands on.
- Could Transformers benefit from ditching attention, altogether? Yann Dauphin and collaborators’ recent work suggests an alternative ConvNet architecture. Transformers, too, might ultimately be doing something similar to ConvNets!
Choosing the right language model for your NLP use-case: key takeaways
- Some key takeaways for LLM selection and deployment:
- When evaluating potential models, be clear about where you are in your AI journey:
- In the beginning, it might be a good idea to experiment with LLMs deployed via cloud APIs.
- Once you have found product-market fit, consider hosting and maintaining your model on your side to have more control and further sharpen model performance to your application.
- To align with your downstream task, your AI team should create a short list of models based on the following criteria:
- Benchmarking results in the academic literature, with a focus on your downstream task.
- Alignment between the pre-training objective and downstream task: consider auto-encoding for NLU and autoregression for NLG. The figure below shows the best LLMs depending on the NLP use-case (image source):

- The short-listed models should be then tested against your real-world task and dataset to get a first feeling for the performance.
- In most cases, you are likely to achieve better quality with dedicated fine-tuning. However, consider few/zero-shot learning if you don’t have the internal tech skills or budget for fine-tuning, or if you need to cover a large number of tasks.
- LLM innovations and trends are short-lived. When using language models, keep an eye on their lifecycle and the overall activity in the LLM landscape and watch out for opportunities to step up your game.
- When evaluating potential models, be clear about where you are in your AI journey:
Transformers Learning Recipe
- Transformers have accelerated the development of new techniques and models for natural language processing (NLP) tasks. While it has mostly been used for NLP tasks, it is now seeing heavy adoption in other areas such as computer vision and reinforcement learning. That makes it one of the most important modern concepts to understand and be able to apply.
- A lot of machine learning and NLP students and practitioners are keen on learning about transformers. Therefore, this recipe of resources and study materials should be helpful to help guide students interested in learning about the world of Transformers.
- To dive deep into the Transformer architecture from an NLP perspective, here’s a few links to better understand and implement transformer models from scratch.
Transformers From Scratch
-
First, try to get a very high-level introduction about transformers. Some references worth looking at:
- Transformers From Scratch (by Brandon Rohrer)
- How Transformers work in deep learning and NLP: an intuitive introduction (by AI Summer)
- Deep Learning for Language Understanding (by DeepMind)
The Illustrated Transformer
- Jay Alammar’s illustrated explanations are exceptional. Once you get that high-level understanding of transformers, going through The Illustrated Transformer is recommend for its detailed and illustrated explanation of transformers:

Lilian Weng’s The Transformer Family
- At this point, you may be looking for a technical summary and overview of transformers. Lilian Weng’s The Transformer Family is a gem and provides concise technical explanations/summaries:
The Annotated Transformer
- Once you’ve absorbed the theory, implementing algorithms from scratch is a great way to test your knowledge and understanding of the subject matter.
- For implementing transformers in PyTorch, The Annotated Transformer offers a great tutorial. Mina Ghashami’s Transformer: Concept and Code from Scratch is also a great resource.
- For implementing transformers in TensorFlow, Transformer model for language understanding offers a great tutorial.
- Google Colab; GitHub
Attention Is All You Need
- This paper by Vaswani et al. introduced the Transformer architecture. Read it after you have a high-level understanding and want to get into the details. Pay attention to other references in the paper for diving deep.
HuggingFace Encoder-Decoder Models
- With the HuggingFace Encoder-Decoder class, you no longer need to stick to pre-built encoder-decoder models like BART or T5, but can instead build your own Encoder-Decoder architecture by doing a mix-and-match with the encoder and decoder model of your choice (similar to stacking legos!), say BERT-GPT2. This is called “warm-starting” encoder-decoder models. Read more here: HuggingFace: Leveraging Pre-trained Language Model Checkpoints for Encoder-Decoder Models.
- You could build your own multimodal encoder-decoder architectures by mixing and matching encoders and decoders. For example:
- Image captioning: ViT/DEiT/BEiT + GPTx
- OCR: ViT/DEiT/BEiT + xBERT
- Image-to-Text (CLIP): ViT/DEiT/BEiT + xBERT
- Speech-to-Text: Wav2Vec2 Encoder + GPTx
- Text-to-Image (DALL-E): xBERT + DALL-E
- Text-to-Speech: xBERT + speech decoder
- Text-to-Image: xBERT + image decoder
- As an example, refer TrOCR: Transformer-based Optical Character Recognition with Pre-trained Models and Leveraging Pre-trained Checkpoints for Sequence Generation Tasks.
Transformers library by HuggingFace
- After some time studying and understanding the theory behind transformers, you may be interested in applying them to different NLP projects or research. At this time, your best bet is the Transformers library by HuggingFace.
- The Hugging Face Team has also published a new book on NLP with Transformers, so you might want to check that out as well.

Inference Arithmetic
- This blog by Kipply presents detailed few-principles reasoning about large language model inference performance, with no experiments or difficult math. The amount of understanding that can be acquired this way is really impressive and practical! A very simple model of latency for inference turns out to be a good fit for emprical results. It can enable better predictions and form better explanations about transformer inference.
Transformer Taxonomy
- This blog by Kipply is a comprehensive literature review of AI, specifically focusing on transformers. It covers 22 models, 11 architectural changes, 7 post-pre-training techniques, and 3 training techniques. The review is curated based on the author’s knowledge and includes links to the original papers for further reading. The content is presented in a loosely ordered manner based on importance and uniqueness.
GPT in 60 Lines of NumPy
- The blog post implements picoGPT and flexes some of the benefits of JAX: (i) trivial to port Numpy using
jax.numpy, (ii) get gradients, and (iii) batch withjax.vmap. It also inferences GPT-2 checkpoints.
x-transformers
- This Github repo offers a concise but fully-featured transformer, complete with a set of promising experimental features from various papers.
Speeding up the GPT - KV cache
- The blog post discusses an optimization technique for speeding up transformer model inference using Key-Value (KV) caching, highlighting its implementation in GPT models to reduce computational complexity from quadratic to linear by caching inputs for the attention block, thereby enhancing prediction speed without compromising output quality.
Transformer Poster
- A poster by Hendrik Erz that goes over how the Transformer works.
FAQs
Did the original Transformer use absolute or relative positional encoding?
- The original Transformer model, as introduced by Vaswani et al. in their 2017 paper “Attention Is All You Need”, used absolute positional encoding. This design was a key feature to incorporate the notion of sequence order into the model’s architecture.
- Absolute Positional Encoding in the Original Transformer
- Mechanism:
- The Transformer model does not inherently capture the sequential order of the input data in its self-attention mechanism. To address this, the authors introduced absolute positional encoding.
- Each position in the sequence was assigned a unique positional encoding vector, which was added to the input embeddings before they were fed into the attention layers.
- Implementation: The positional encodings used were fixed (not learned) and were based on sine and cosine functions of different frequencies. This choice was intended to allow the model to easily learn to attend by relative positions since for any fixed offset \(k, PE_{pos + k}\) could be represented as a linear function of \(PE_{pos}\).
- Mechanism:
- Importance: This approach to positional encoding was crucial for enabling the model to understand the order of tokens in a sequence, a fundamental aspect of processing sequential data like text.
- Relative and Rotary Positional Encoding in Later Models
- After the introduction of the original Transformer, subsequent research explored alternative ways to incorporate positional information. One such development was the use of relative positional encoding, which, instead of assigning a unique encoding to each absolute position, encodes the relative positions of tokens with respect to each other. This method has been found to be effective in certain contexts and has been adopted in various Transformer-based models developed after the original Transformer. Rotary positional encoding methods (such as RoPE) were also presented after relative positional encoding methods.
- Conclusion: In summary, the original Transformer model utilized absolute positional encoding to integrate sequence order into its architecture. This approach was foundational in the development of Transformer models, while later variations and improvements, including relative positional encoding, have been explored in subsequent research to further enhance the model’s capabilities.
How does the choice of positional encoding method can influence the number of parameters added to the model? Consinder absolute, relative, and rotary positional encoding mechanisms.
- In Large Language Models (LLMs), the choice of positional encoding method can influence the number of parameters added to the model. Let’s compare absolute, relative, and rotary (RoPE) positional encoding in this context:
- Absolute Positional Encoding
- Parameter Addition:
- Absolute positional encodings typically add a fixed number of parameters to the model, depending on the maximum sequence length the model can handle.
- Each position in the sequence has a unique positional encoding vector. If the maximum sequence length is \(N\) and the model dimension is \(D\), the total number of added parameters for absolute positional encoding is \(N \times D\).
- Fixed and Non-Learnable: In many implementations (like the original Transformer), these positional encodings are fixed (based on sine and cosine functions) and not learnable, meaning they don’t add to the total count of trainable parameters.
- Parameter Addition:
- Relative Positional Encoding
- Parameter Addition:
- Relative positional encoding often adds fewer parameters than absolute encoding, as it typically uses a set of parameters that represent relative positions rather than unique encodings for each absolute position.
- The exact number of added parameters can vary based on the implementation but is generally smaller than the \(N \times D\) parameters required for absolute encoding.
- Learnable or Fixed: Depending on the model, relative positional encodings can be either learnable or fixed, which would affect whether they contribute to the model’s total trainable parameters.
- Parameter Addition:
- Rotary Positional Encoding (RoPE)
- Parameter Addition:
- RoPE does not add any additional learnable parameters to the model. It integrates positional information through a rotation operation applied to the query and key vectors in the self-attention mechanism.
- The rotation is based on the position but is calculated using fixed, non-learnable trigonometric functions, similar to absolute positional encoding.
- Efficiency: The major advantage of RoPE is its efficiency in terms of parameter count. It enables the model to capture relative positional information without increasing the number of trainable parameters.
- Parameter Addition:
- Summary:
- Absolute Positional Encoding: Adds \(N \times D\) parameters, usually fixed and non-learnable.
- Relative Positional Encoding: Adds fewer parameters than absolute encoding, can be learnable, but the exact count varies with implementation.
- Rotary Positional Encoding (RoPE): Adds no additional learnable parameters, efficiently integrating positional information.
- In terms of parameter efficiency, RoPE stands out as it enriches the model with positional awareness without increasing the trainable parameter count, a significant advantage in the context of LLMs where managing the scale of parameters is crucial.
In Transformer-based models, why is RoPE required for context length extension?
- RoPE, or Rotary Positional Embedding, is a technique used in some language models, particularly Transformers, for handling positional information. The need for RoPE or similar techniques becomes apparent when dealing with long context lengths in Large Language Models (LLMs).
- Context Length Extension in LLMs
- Positional Encoding in Transformers:
- Traditional Transformer models use positional encodings to add information about the position of tokens in a sequence. This is crucial because the self-attention mechanism is, by default, permutation-invariant (i.e., it doesn’t consider the order of tokens).
- In standard implementations like the original Transformer, positional encodings are added to the token embeddings and are typically fixed (not learned) and based on sine and cosine functions of different frequencies.
- Challenges with Long Sequences: As the context length (number of tokens in a sequence) increases, maintaining effective positional information becomes challenging. This is especially true for fixed positional encodings, which may not scale well or capture relative positions effectively in very long sequences.
- Role and Advantages of RoPE
- Rotary Positional Embedding: RoPE is designed to provide rotational equivariance to self-attention. It essentially encodes the absolute position and then rotates the positional encoding of keys and queries differently based on their position. This allows the model to implicitly capture relative positional information through the self-attention mechanism.
- Effectiveness in Long Contexts: RoPE scales effectively with sequence length, making it suitable for LLMs that need to handle long contexts or documents. This is particularly important in tasks like document summarization or question-answering over long passages.
- Preserving Relative Positional Information: RoPE allows the model to understand the relative positioning of tokens effectively, which is crucial in understanding the structure and meaning of sentences, especially in languages with less rigid syntax.
- Computational Efficiency: Compared to other methods of handling positional information in long sequences, RoPE can be more computationally efficient, as it doesn’t significantly increase the model’s complexity or the number of parameters.
- Conclusion: In summary, RoPE is required for effectively extending the context length in LLMs due to its ability to handle long sequences while preserving crucial relative positional information. It offers a scalable and computationally efficient solution to one of the challenges posed by the self-attention mechanism in Transformers, particularly in scenarios where understanding the order and relationship of tokens in long sequences is essential.
Why is the Transformer Architecture not as susceptible to vanishing gradients compared to RNNs?
- The Transformer architecture is less susceptible to vanishing gradients compared to Recurrent Neural Networks (RNNs) due to several key differences in their design and operation:
- Self-Attention Mechanism and Parallel Processing:
- Transformers: Transformers use self-attention mechanisms which allow them to directly access any position in the input sequence without the need for sequential processing. This means that the gradients can flow more easily across the entire network since there are direct connections between all input and output positions. Additionally, the self-attention mechanism and feed-forward layers in Transformers allow for parallel processing of the entire sequence, facilitating better gradient flow and more efficient training. To handle the sequential nature of data, Transformers use positional encodings added to the input embeddings, enabling them to maintain the order of the sequence while still allowing parallel processing.
- RNNs: RNNs process input sequences sequentially, step by step. This sequential processing can cause gradients to either vanish or explode as they are propagated back through many time steps during training, especially in long sequences. RNNs are typically trained using Backpropagation Through Time (BPTT), a method that unrolls the network through time and applies backpropagation. BPTT can suffer from vanishing and exploding gradients because the gradients must be propagated back through many time steps, leading to instability and difficulty in training long sequences.
- Residual Connections:
- Transformers: Each layer in a Transformer includes residual (skip) connections, which add the input of a layer to its output. These connections help gradients flow through the network more directly, mitigating the vanishing gradient problem.
- RNNs: Although some RNN architectures can incorporate residual connections, it is less common and less effective due to the inherently sequential nature of RNNs.
- Layer Normalization:
- Transformers: Transformers use layer normalization, which helps stabilize the training process and maintain gradient magnitudes.
- RNNs: While batch normalization and layer normalization can be applied to RNNs, it is more challenging and less common compared to the straightforward application in Transformers.
- Self-Attention Mechanism and Parallel Processing:
- In summary, the Transformer architecture’s reliance on parallel processing nature of self-attention (and thus the avoidance of BPTT that RNNs depend on), residual connections, and layer normalization contributes to its robustness against vanishing gradients, making it more efficient and effective for handling long sequences compared to RNNs.
What is the fraction of attention weights relative to feed-forward weights in common LLMs?
GPT
- In GPT-1 and similar transformer-based models, the distribution of parameters between attention mechanisms and feed-forward networks (FFNs) is key to understanding their architecture and design. Let’s delve into the parameter allocation in GPT-1:
Model Configuration
-
GPT-1, like many models in the GPT series, follows the transformer architecture described in the original “Attention is All You Need” paper. Here’s a breakdown:
- Model Dimension (\(d_{\text{model}}\)): For GPT-1, \(d_{\text{model}}\) is typically smaller compared to later models like GPT-3. The size used in GPT-1 is 768.
- Feed-Forward Dimension (\(d_{\text{ff}}\)): The dimension of the feed-forward layers in GPT-1 is typically about 4 times the model dimension, similar to other transformers. This results in \(d_{\text{ff}} = 3072\) for GPT-1.
Attention and Feed-Forward Weights Calculation
-
Let’s calculate the typical number of parameters for each component:
- Attention Parameters:
- Query, Key, Value (QKV) Weights: Each transformer layer in GPT-1 includes multi-head self-attention with separate weights for queries, keys, and values. Each of these matrices is of size \(d_{\text{model}} \times \frac{d_{\text{model}}}{h}\), and for simplicity, the total size for Q, K, and V combined for all heads is \(d_{\text{model}} \times d_{\text{model}}\).
- Output Projection: This is another matrix of size \(d_{\text{model}} \times d_{\text{model}}\).
- Feed-Forward Network (FFN) Parameters:
- Layer Projections: Consisting of two linear transformations:
- First layer projects from \(d_{\text{model}}\) to \(d_{\text{ff}}\),
- Second layer projects back from \(d_{\text{ff}}\) to \(d_{\text{model}}\).
- Layer Projections: Consisting of two linear transformations:
Example Calculation with GPT-1 Values
- Total Attention Weights Per Layer:
- Total for Q, K, and V combined: \(768 \times 768 \times 3 = 1769472\).
- Output projection: \(768 \times 768 = 589824\).
- Total attention weights: \(1769472 + 589824 = 2359296\) parameters.
- Total Feed-Forward Weights Per Layer:
- Up-projection: \(768 \times 3072 = 2359296\),
- Down-projection: \(3072 \times 768 = 2359296\),
- Total FFN weights: \(2359296 + 2359296 = 4718592\) parameters.
Fraction of Attention to FFN Weights
- The fraction of attention weights relative to FFN weights can be calculated as:
Conclusion
- In GPT-1, the feed-forward networks hold about twice as many parameters as the attention mechanisms, a typical distribution for transformer models. This emphasizes the substantial role of the FFNs in enhancing the model’s ability to process and transform information, complementing the capabilities provided by the attention mechanisms. This balance is crucial for the overall performance and flexibility of the model in handling various language processing tasks.
GPT-2
- In common large language models like GPT-2, the fraction of attention weights relative to feed-forward (MLP) weights generally follows a consistent pattern due to the architecture of the transformer layers used in these models. Typically, the Multi-Layer Perceptron (MLP) blocks contain significantly more parameters than the attention blocks.
- Here’s a breakdown for better understanding:
Transformer Layer Composition
- Attention Mechanism: Each layer in a transformer-based model like GPT-2 includes multi-head self-attention mechanisms. The parameters in these mechanisms consist of query, key, value, and output projection matrices.
- Feed-Forward Network (MLP): Following the attention mechanism, each layer includes an MLP block, typically consisting of two linear transformations with a ReLU activation in between.
Parameter Distribution
- Attention Weights: For each attention head, the parameters are distributed across the matrices for queries, keys, values, and the output projection. If the model dimension is \(d_{\text{model}}\) and there are \(h\) heads, each head might use matrices of size \(\frac{d_{\text{model}}}{h} \times d_{\text{model}}\) for each of the query, key, and value, and \(d_{\text{model}} \times d_{\text{model}}\) for the output projection.
- MLP Weights: The MLP usually consists of two layers. The first layer projects from \(d_{\text{model}}\) to \(d_{\text{ff}}\) (where \(d_{\text{ff}}\) is typically 4 times \(d_{\text{model}}\)), and the second layer projects back from \(d_{\text{ff}}\) to \(d_{\text{model}}\). Thus, the MLP contains weights of size \(d_{\text{model}} \times d_{\text{ff}}\) and \(d_{\text{ff}} \times d_{\text{model}}\).
Example Calculation
- For GPT-2, if we assume \(d_{\text{model}} = 768\) and \(d_{\text{ff}} = 3072\) (which is common in models like GPT-2), and the number of heads \(h = 12\):
- Attention Parameters per Layer: Each set of Q/K/V matrices is \(\frac{768}{12} \times 768 = 49152\) parameters, and there are 3 sets per head, plus another \(768 \times 768\) for the output projection, totaling \(3 \times 49152 + 589824 = 737280\) parameters for all attention heads combined per layer.
- MLP Parameters per Layer: \(768 \times 3072 + 3072 \times 768 = 4718592\) parameters.
Fraction of Attention to MLP Weights
-
Fraction: Given these typical values, the attention parameters are about 737280, and the MLP parameters are about 4718592 per layer. This gives a fraction of attention to MLP weights of roughly \(\frac{737280}{4718592} \approx 0.156\), or about 15.6%.
-
This fraction indicates that the feed-forward layers in models like GPT-2 hold a substantially larger portion of the parameters compared to the attention mechanisms, emphasizing the role of the MLP in transforming representations within the network. This distribution has implications for deciding which components to adapt or optimize during tasks like fine-tuning, as the MLP layers may offer a larger scope for modification due to their greater parameter count.
BERT
- In the architecture of BERT (Bidirectional Encoder Representations from Transformers), which utilizes the transformer model structure similar to models in the GPT series, the distribution of parameters between attention mechanisms and feed-forward networks (FFNs) reflects a balance that is integral to the model’s ability to perform its intended tasks. Here’s an overview of how these weights are typically distributed in BERT and similar models:
Model Configuration
- Model Dimension (\(d_{\text{model}}\)): This is the size of the hidden layers throughout the model. For example, BERT-Base uses \(d_{\text{model}} = 768\).
- Feed-Forward Dimension (\(d_{\text{ff}}\)): The dimension of the feed-forward layer is usually set to about 4 times \(d_{\text{model}}\). For BERT-Base, \(d_{\text{ff}} = 3072\).
Attention and Feed-Forward Weights Calculation
- Attention Parameters:
- Query, Key, Value (QKV) Weights: Each transformer layer in BERT has multi-head self-attention with separate weights for queries, keys, and values. For each head:
- Size of each matrix (Q, K, V): \(d_{\text{model}} \times \frac{d_{\text{model}}}{h}\), where \(h\) is the number of heads. The total size per matrix type for all heads combined is \(d_{\text{model}} \times d_{\text{model}}\).
- Output Projection Weights: Another matrix of size \(d_{\text{model}} \times d_{\text{model}}\).
- Query, Key, Value (QKV) Weights: Each transformer layer in BERT has multi-head self-attention with separate weights for queries, keys, and values. For each head:
- Feed-Forward Network (FFN) Parameters:
- Layer Projections: There are two linear transformations in the FFN block:
- The first layer projects from \(d_{\text{model}}\) to \(d_{\text{ff}}\),
- The second layer projects back from \(d_{\text{ff}}\) to \(d_{\text{model}}\).
- Layer Projections: There are two linear transformations in the FFN block:
Example Calculation with Typical Values
- Attention Weights Per Layer:
- For Q, K, and V: \(768 \times 768 \times 3 = 1769472\) (each type has size \(768 \times 768\)).
- Output projection: \(768 \times 768 = 589824\).
- Total Attention Weights: \(1769472 + 589824 = 2359296\) parameters.
- Feed-Forward Weights Per Layer:
- Up-projection: \(768 \times 3072 = 2359296\),
- Down-projection: \(3072 \times 768 = 2359296\),
- Total FFN Weights: \(2359296 + 2359296 = 4718592\) parameters.
Fraction of Attention to FFN Weights
- The fraction of attention weights relative to FFN weights can be calculated as:
Conclusion
- In BERT, like in many transformer models, the feed-forward networks hold about twice as many parameters as the attention mechanisms. This indicates a strong emphasis on the transformation capabilities of the FFNs, crucial for enabling BERT to generate context-rich embeddings for various NLP tasks. The FFN layers in BERT and similar models play a pivotal role in enhancing the model’s representational power, ensuring it can handle complex dependencies and nuances in language understanding and generation tasks.
In BERT, how do we go from \(Q\), \(K\), and \(V\) at the final transformer block’s output to contextualized embeddings?
- To understand how the \(Q\), \(K\), and \(V\) matrices contribute to the contextualized embeddings in BERT, let’s dive into the core processes occurring in the final layer of BERT’s transformer encoder stack. Each layer performs self-attention, where the matrices \(Q\), \(K\), and \(V\) interact to determine how each token attends to others in the sequence. Through this mechanism, each token’s embedding is iteratively refined across multiple layers, progressively capturing both its own attributes and its contextual relationships with other tokens.
- By the time these computations reach the final layer, the output embeddings for each token are highly contextualized. Each token’s embedding now encapsulates not only its individual meaning but also the influence of surrounding tokens, providing a rich representation of the token in context. This final, refined embedding is what BERT ultimately uses to represent each token, balancing individual token characteristics with the nuanced context in which the token appears.
-
Let’s dive deeper into how the \(Q\), \(K\), and \(V\) matrices at each layer ultimately yield embeddings that are contextualized, particularly by looking at what happens in the final layer of BERT’s transformer encoder stack. The core steps involved from self-attention outputs in the last layer to meaningful embeddings per token are:
-
Self-Attention Mechanism Recap:
- In each layer, BERT computes self-attention across the sequence of tokens. For each token, it generates a query vector \(Q\), a key vector \(K\), and a value vector \(V\). These matrices are learned transformations of the token embeddings and encode how each token should attend to other tokens.
- For each token in the sequence, self-attention calculates attention scores by comparing \(Q\) with \(K\), determining the influence or weight of other tokens relative to the current token.
-
Attention Weights Calculation:
- For each token, the model computes the similarity of its \(Q\) vector with every other token’s \(K\) vector in the sequence. This similarity score is then normalized (typically through softmax), resulting in attention weights.
- These weights tell us the degree to which each token should “attend to” (or incorporate information from) other tokens.
-
Weighted Summation of Values (Producing Contextual Embeddings):
- Using the attention weights, each token creates a weighted sum over the \(V\) vectors of other tokens. This weighted sum serves as the output of the self-attention operation for that token.
- Each token’s output is thus a combination of other tokens’ values, weighted by their attention scores. This result effectively integrates context from surrounding tokens.
-
Passing Through Multi-Head Attention and Feed-Forward Layers:
- BERT uses multi-head attention, meaning that it performs multiple attention computations (heads) in parallel with different learned transformations of \(Q\), \(K\), and \(V\).
- Each head provides a different “view” of the relationships between tokens. The outputs from all heads are concatenated and then passed through a feed-forward layer to further refine each token’s representation.
-
Stacking Layers for Deeper Contextualization:
- The output from the multi-head attention and feed-forward layer for each token is passed as input to the next layer. Each subsequent layer refines the token embeddings by adding another layer of attention-based contextualization.
- By the final layer, each token embedding has been repeatedly updated, capturing nuanced dependencies from all tokens in the sequence through multiple self-attention layers.
-
Extracting Final Token Embeddings from the Last Encoder Layer:
- After the last layer, the output matrix contains a contextualized embedding for each token in the sequence. These embeddings represent the final “meaning” of each token as understood by BERT, based on the entire input sequence.
- For a sequence with \(n\) tokens, the output from the final layer is a matrix of shape \(n \times d\), where \(d\) is the embedding dimension.
-
Embedding Interpretability and Usage:
- The embedding for each token in this final matrix is now contextualized; it reflects not just the identity of the token itself but also its role and relationships within the context of the entire sequence.
- These final embeddings can be used for downstream tasks, such as classification or question answering, where the model uses these embeddings to predict task-specific outputs.
What gets passed on from the output of the previous transformer block to the next in the encoder/decoder?
-
In a transformer-based architecture (such as the vanilla transformer or BERT), the output of each transformer block (or layer) becomes the input to the subsequent layer in the stack. Specifically, here’s what gets passed from one layer to the next:
-
Token Embeddings (Contextualized Representations):
- The main component passed between layers is a set of token embeddings, which are contextualized representations of each token in the sequence up to that layer.
- For a sequence of \(n\) tokens, if the embedding dimension is \(d\), the output of each layer is an \(n \times d\) matrix, where each row represents the embedding of a token, now updated with contextual information learned from the previous layer.
- Each embedding at this point reflects the token’s meaning as influenced by the other tokens it attended to in that layer.
-
Residual Connections:
- Transformers use residual connections to stabilize training and allow better gradient flow. Each layer’s output is combined with its input via a residual (or skip) connection.
- In practice, the output of the self-attention and feed-forward operations is added to the input embeddings from the previous layer, preserving information from the initial representation.
-
Layer Normalization:
- After the residual connection, layer normalization is applied to the summed representation. This normalization helps stabilize training by maintaining consistent scaling of token representations across layers.
- The layer-normalized output is then what gets passed on as the “input” to the next layer.
-
Positional Information:
- The positional embeddings (added initially to the token embeddings to account for the order of tokens in the sequence) remain embedded in the representations throughout the layers. No additional positional encoding is added between layers; instead, the attention mechanism itself maintains positional relationships indirectly.
-
Summary of the Process:
- Each layer receives an \(n \times d\) matrix (the sequence of token embeddings), which now includes contextual information from previous layers.
- The layer performs self-attention and passes the output through a feed-forward network.
- The residual connection adds the original input to the output of the feed-forward network.
- Layer normalization is applied to this result, and the final matrix is passed on as the input to the next layer.
- This flow ensures that each successive layer refines the contextual embeddings for each token, building progressively more sophisticated representations of tokens within the context of the entire sequence.
In the vanilla transformer, what gets passed on from the output of the encoder to the decoder?
- In the original (vanilla) Transformer model, the encoder processes the input sequence and produces a sequence of encoded representations, often referred to as “encoder output” or “memory.” This encoder output is then fed into each layer of the decoder to help it generate the target sequence.
-
Specifically:
-
Encoder Output as Memory: After the encoder processes the input sequence through multiple layers, it outputs a sequence of vectors (one for each input token). These vectors capture context and relationships between tokens, enriched by the attention mechanism. This entire set of vectors is passed to the cross-attention (i.e., unmasked/non-causal) attention layer in each decoder block.
-
Cross-Attention in the Decoder: In each decoder block, there is a cross-attention mechanism that takes the encoder output as “keys” and “values,” while the decoder’s own output (from the previous layer) serves as the “query.” This cross-attention step enables the decoder to focus on relevant parts of the encoder’s output, effectively allowing it to “look back” at the encoded input sequence when generating each token in the output.
-
Final Decoder Output: After the decoder processes its input through several Transformer blocks—with each block having with its own self-attention layer, cross-attention layer, and feed-forward layer produces a sequence of output vectors, which are used to predict the next tokens in the target sequence.
-
- In summary, the encoder output serves as the source of information for the decoder, allowing it to access context from the input sequence through cross-attention in each decoder layer.
Further Reading
- The Illustrated Transformer
- The Annotated Transformer
- Transformer models: an introduction and catalog
- Deep Learning for NLP Best Practices
- What is Teacher Forcing for Recurrent Neural Networks?
- What is Teacher Forcing?
- The Transformer Family
- Transformer: Concept and Code from Scratch
- Transformer Inference Arithmetic
- Transformer Taxonomy
References
- Transformers are Graph Neural Networks
- Transformers from Scratch by Brandon Rohrer
- Transformers from Scratch by Peter Bloem
- Positional encoding tutorial by Amirhossein Kazemnejad
- What is One Hot Encoding? Why and When Do You Have to Use it?
- Wikipedia: Dot product
- Wikipedia: Byte pair encoding
- Will Transformers Take Over Artificial Intelligence?
- Transformer Recipe
- The decoder part in a transformer model
- Why encoder input doesn’t have a start token?
- What is the cost function of a transformer?
- Transformer models: an introduction and catalog
- Why does a transformer not use an activation function following the multi-head attention layer?
- CNN Explainer: Learn Convolutional Neural Network (CNN) in your browser!
- Where is dropout placed in the original transformer?
Citation
If you found our work useful, please cite it as:
@article{Chadha2020DistilledTransformers,
title = {Transformers},
author = {Chadha, Aman},
journal = {Distilled AI},
year = {2020},
note = {\url{https://aman.ai}}
}









